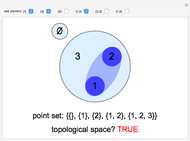
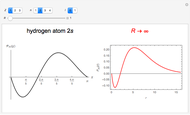
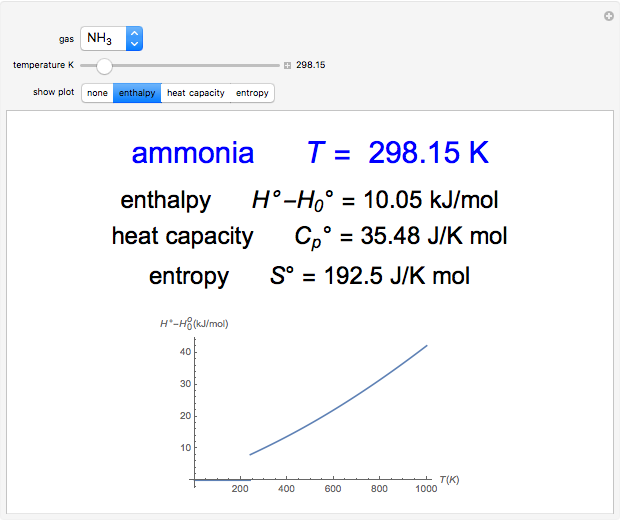
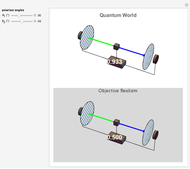
Measurement of Electron e/m Using a Modified Magnetron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
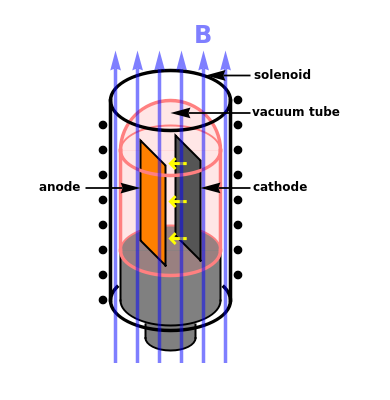
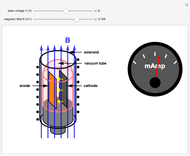
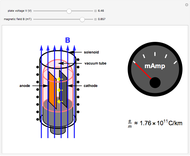
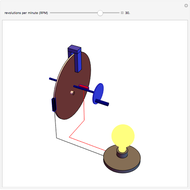
The magnetron is an electronic tube (valve in British) used to produce microwave radiation. It was essential for the Allies' development of radar in World War II and is also the power source for microwave ovens. A functioning magnetron usually operates at voltages too high to be safe for student experiments. Moreover, the sought-after electron  ratio is deeply embedded in the voltage, magnetic-field, and resonant radiation-frequency characteristics.
ratio is deeply embedded in the voltage, magnetic-field, and resonant radiation-frequency characteristics.
Contributed by: S. M. Blinder (March 2011)
After a suggestion by H. K. Nahan
Open content licensed under CC BY-NC-SA
Snapshots
Details
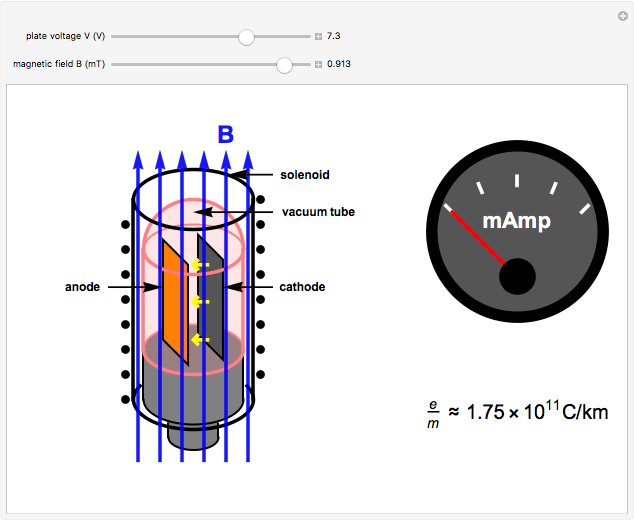
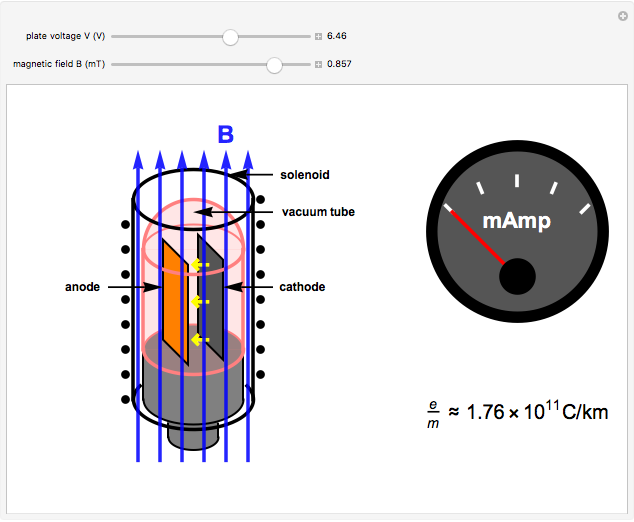
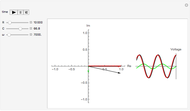
An electron of mass  and charge
and charge  moving in an electric field
moving in an electric field  and a magnetic field
and a magnetic field  is given by the Lorentz force equation
is given by the Lorentz force equation  . For crossed electric and magnetic fields with constant magnitudes, the problem can be simplified. The speed of the electron in an accelerating voltage
. For crossed electric and magnetic fields with constant magnitudes, the problem can be simplified. The speed of the electron in an accelerating voltage  is given by
is given by 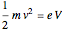 . The perpendicular magnetic field will then deflect the electron into a circular orbit such that
. The perpendicular magnetic field will then deflect the electron into a circular orbit such that  . Eliminating
. Eliminating  between the last two equations gives
between the last two equations gives  . When
. When  , where
, where  is the distance between the anode and cathode (assumed equal to 1 cm), the plate current
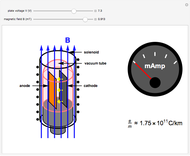
is the distance between the anode and cathode (assumed equal to 1 cm), the plate current  drops to zero. The charge to mass ratio is then given by
drops to zero. The charge to mass ratio is then given by  . The experimental error is in the range of 1%.
. The experimental error is in the range of 1%.
For more information on the magnetron, see http://www.radartutorial.eu/08.transmitters/tx08.en.html.
Permanent Citation