Minkowski Sum of Convex Robot and Obstacle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
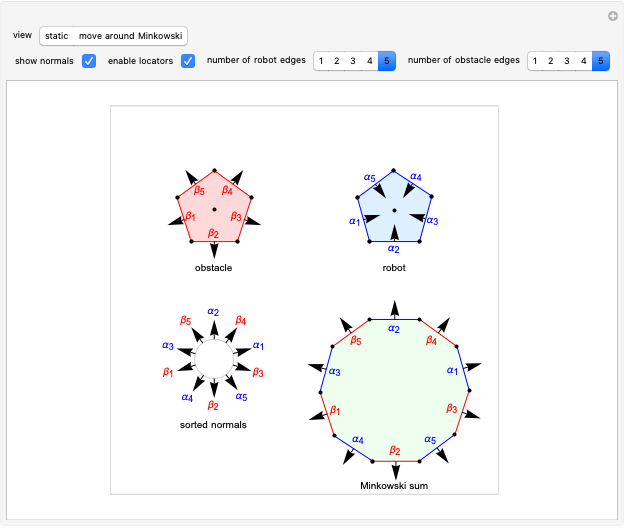
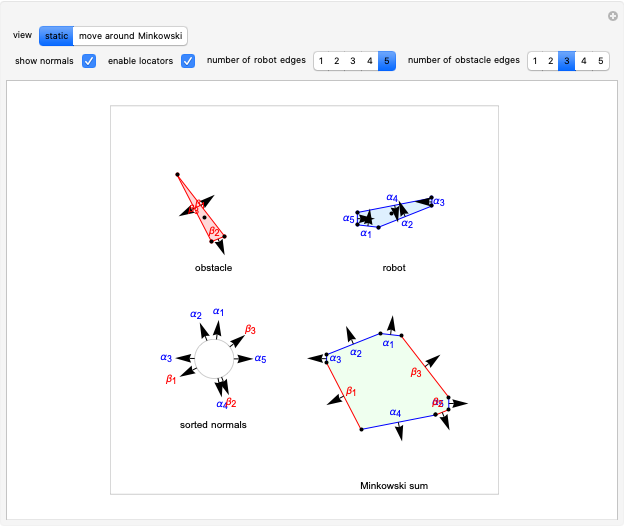
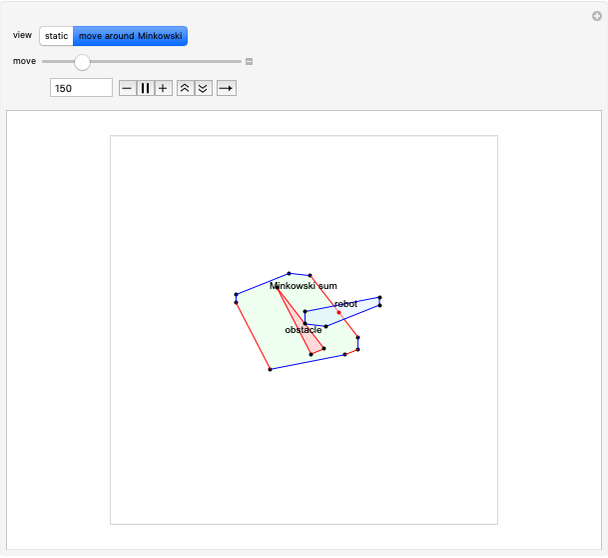
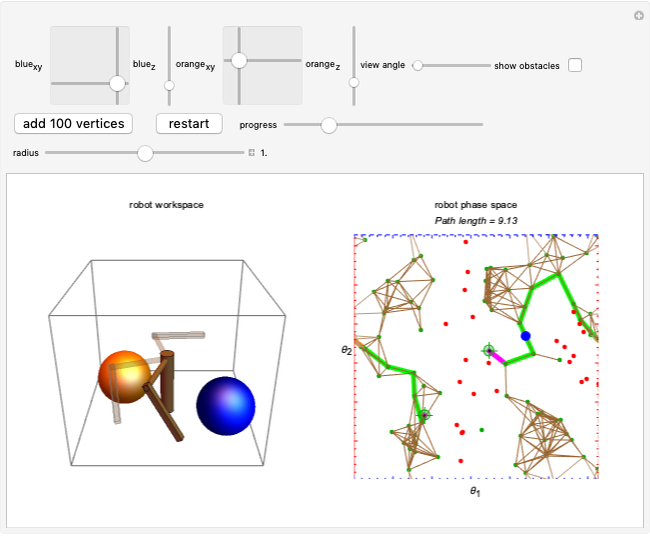
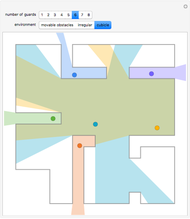
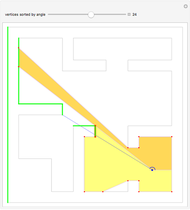
The Minkowski sum of a convex obstacle and a robot delineates the region where an obstacle and a robot might collide. Knowing this region simplifies robot motion planning. Set "view" to "static" and drag the locators to make arbitrary two-dimensional robots and obstacles. The region of the Minkowski sum can be traced out by choosing "move around Minkowski" to animate the robot moving around the edge of the obstacle.
Contributed by: Shreyas Poyrekar, Arifa Sultana and Aaron T. Becker (April 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
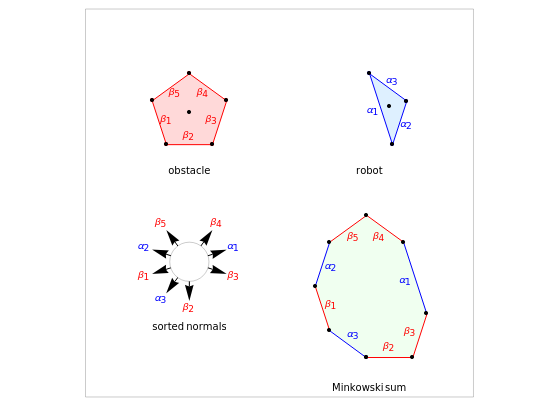
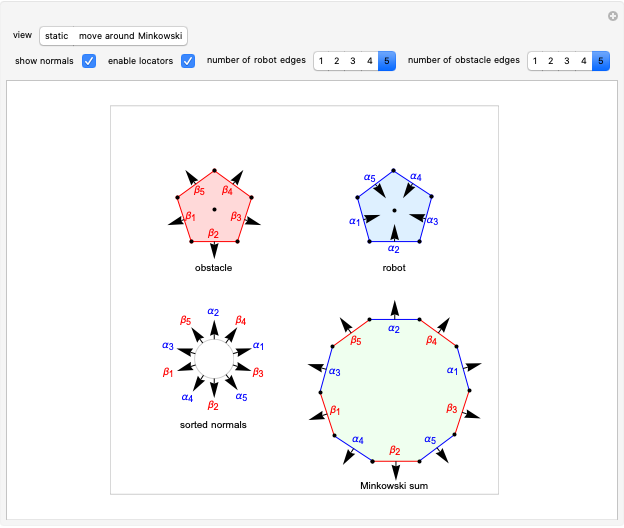
The Minkowski sum is the set of all coordinates in which one polygon overlaps another. It is computed in four easy steps. In the following, we label the stationary polygon the obstacle and the moving polygon the robot.
This version assumes both polygons are convex. First, compute the convex hull of both the polygons, the robot and the obstacle. The obstacle edges are colored red and the robot edges blue.
Second, the normals to the sides of the polygons are drawn. These point outward for the obstacle and inward for the robot.
Third, these normals are sorted in the increasing order of their angles. The lower-left image shows the sorted normals.
The first point in the Minkowski sum is arbitrarily chosen as a point where the centroid of the robot lies at one of the vertex-vertex contacts of the obstacle and robot, assuming the robot is appropriately translated.
Finally, the Minkowski sum is generated by adding each edge in the order specified by the normals. Robot edges are added in the clockwise direction, obstacle edges in the counterclockwise direction. A significant observation is that every edge of the Minkowski sum polygon is a translated edge from either the obstacle or the robot polygon.
The Minkowski sum is useful for robot navigation because, once it is computed, the problem of finding a collision-free path for a polygon-shaped robot moving through a workspace filled with obstacles is reduced to finding a path for a point-shaped robot through a configuration space filled with Minkowski sums.
The Minkowski sum was named after German mathematician Hermann Minkowski (1864–1909).
Reference
[1] S. M. LaValle, Planning Algorithms, New York: Cambridge University Press, 2006.
Permanent Citation