Probabilistic Roadmap Method with Seven-Link Articulated Robot

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
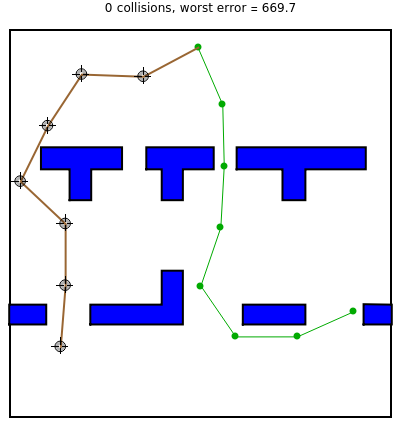
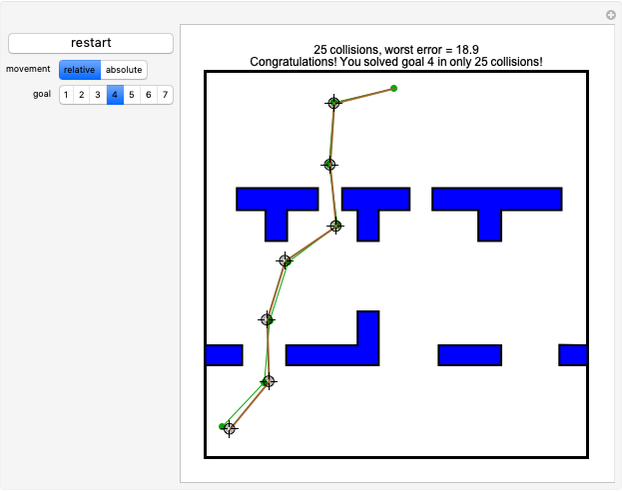
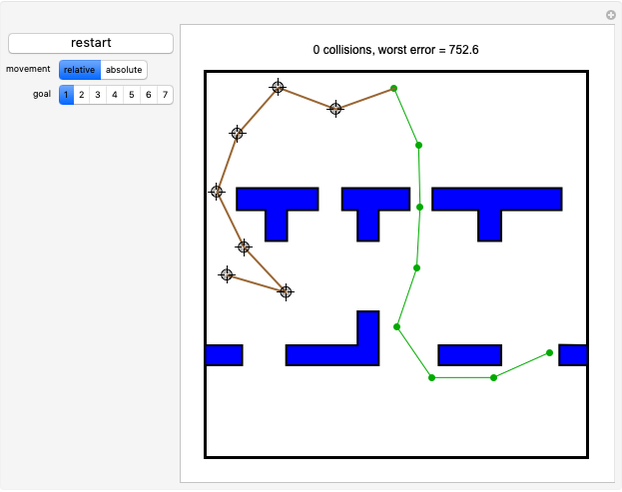
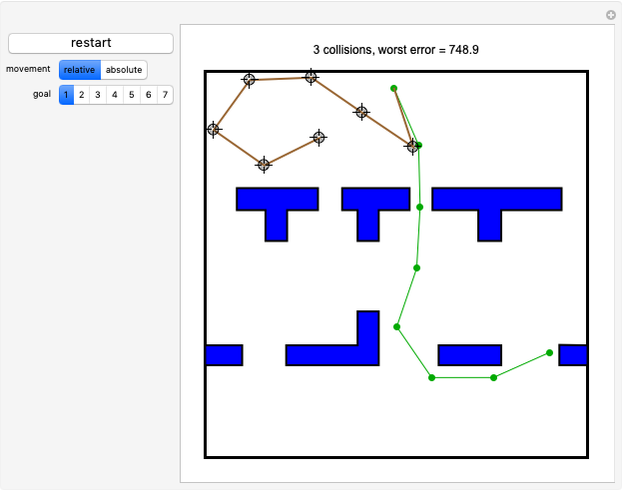
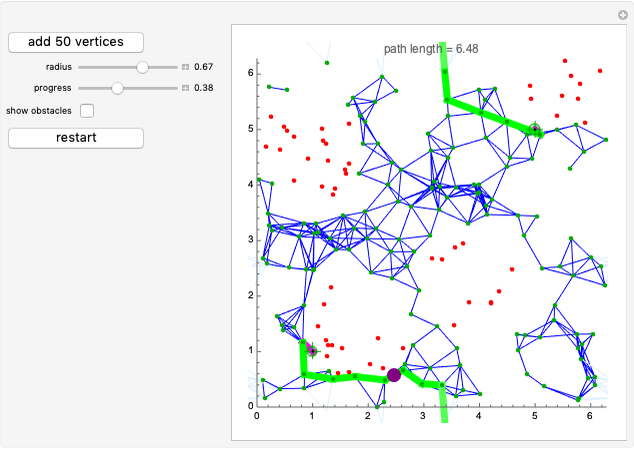
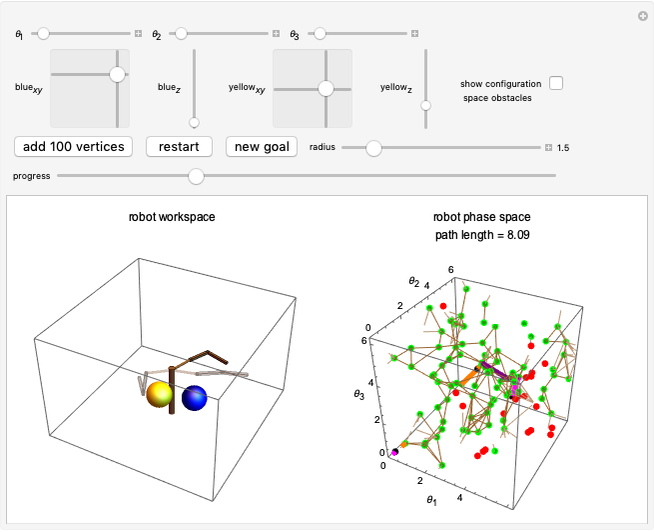
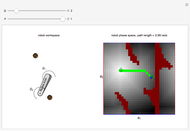
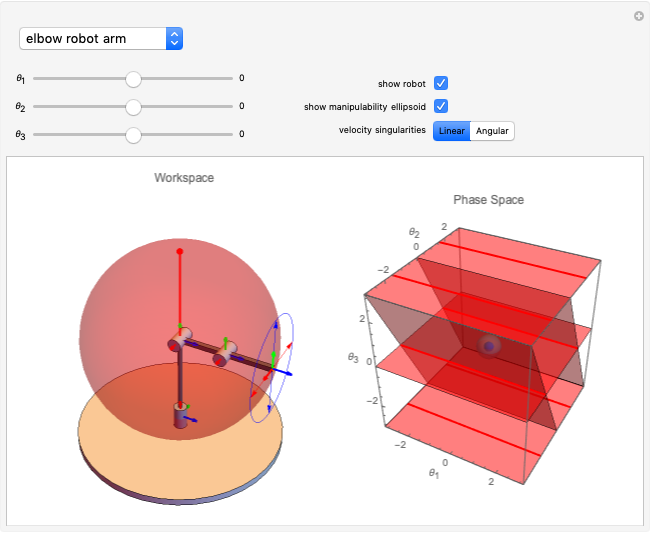
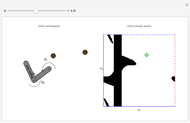
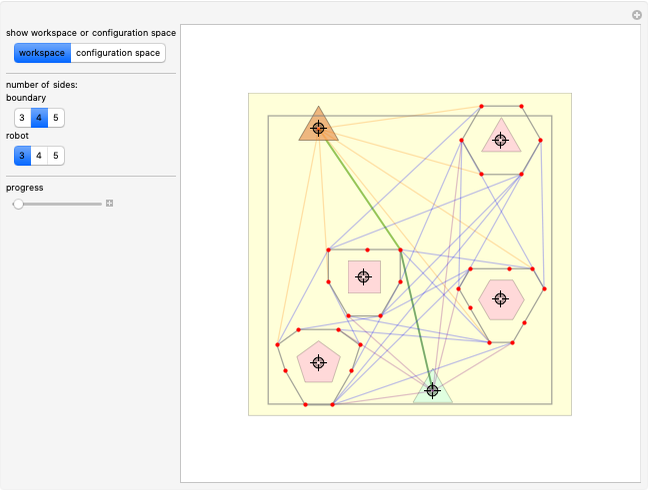
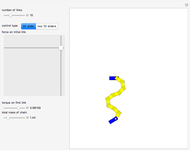
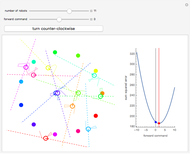
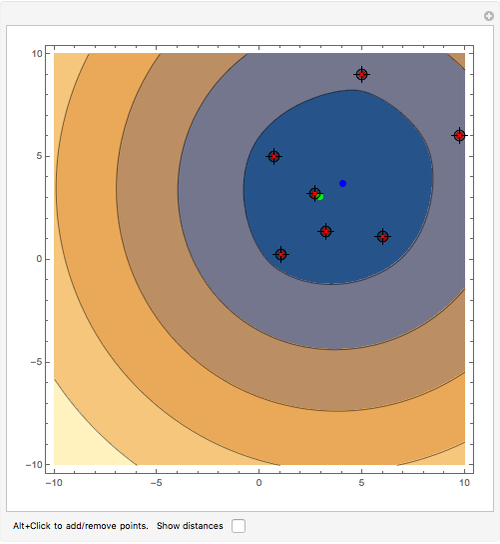
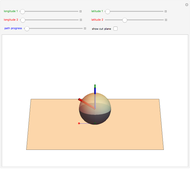
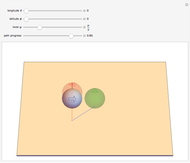
This Demonstration challenges you to move the seven-link robot (in brown) to match a goal configuration (in green) with the minimum number of collisions. Drag the locators to move the robot while avoiding collisions with the blue obstacles. This example was used in 1995 to introduce the probabilistic roadmap method (PRM), a robot motion-planning technique. Selecting "relative" movement changes the angle of one robot link at a time, and "absolute" rotates all subsequent links.
Contributed by: Aaron T. Becker and Yitong Lu (April 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
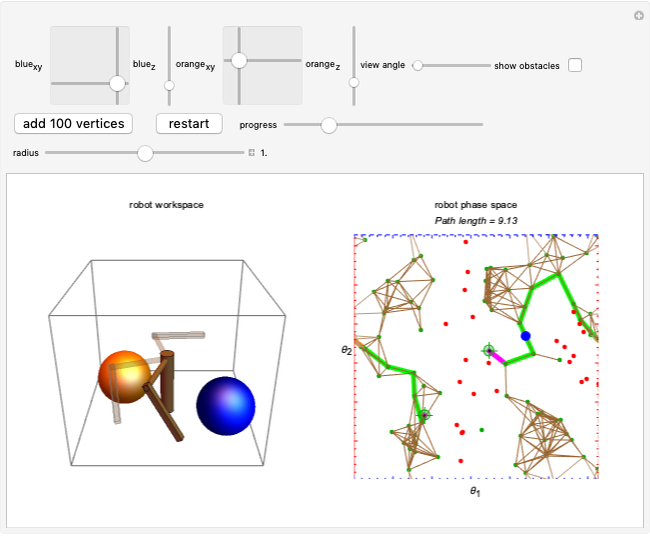
The goal of robot motion planning is to find a continuous path from an initial configuration to a goal configuration that is collision free. A configuration is a complete specification of every point of the robot. This Demonstration uses a seven-link robot with seven rotational joints that can each rotate from 0 to  . The resulting configuration space can be represented as a seven-dimensional torus. Obstacles in the robot's workspace map to obstacle regions in the configuration space, but computing these regions is computationally expensive. Planning for robots in high-dimensional spaces is difficult because representing the connected parts of high-dimensional spaces requires a number of samples that grows exponentially with the dimensionality of the space. This is commonly called "the curse of dimensionality."
. The resulting configuration space can be represented as a seven-dimensional torus. Obstacles in the robot's workspace map to obstacle regions in the configuration space, but computing these regions is computationally expensive. Planning for robots in high-dimensional spaces is difficult because representing the connected parts of high-dimensional spaces requires a number of samples that grows exponentially with the dimensionality of the space. This is commonly called "the curse of dimensionality."
The probabilistic roadmap method (PRM) was developed in 1996 by Lydia Kavraki et al. [1] as a general-purpose technique to solve such problems. Indeed, this Demonstration reproduces Figure 2 from [1]. PRMs generate a random roadmap that can be reused for subsequent motion-planning queries.
Reference
[1] L. E. Kavraki, P. Svestka, J-C. Latombe and M. H. Overmars. "Probabilistic Roadmaps for Path Planning in High-Dimensional Configuration Spaces." IEEE Transactions on Robotics and Automation, 12(4), 1996 pp. 566–580. doi:10.1109/70.508439.
Permanent Citation