Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

On the Areas of Triangles Associated with an Excircle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

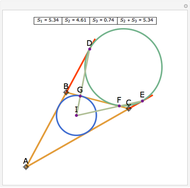
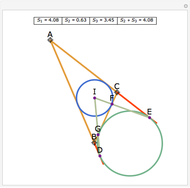
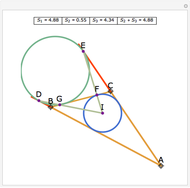
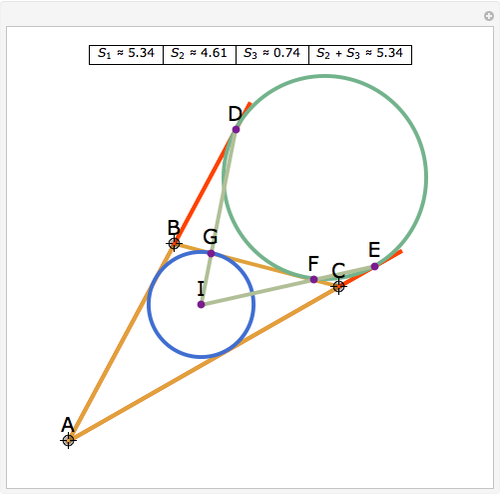
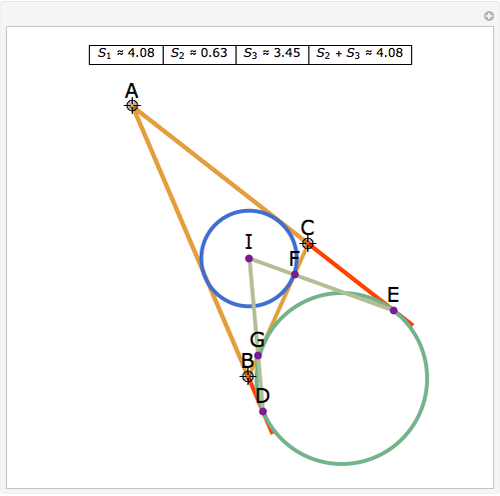
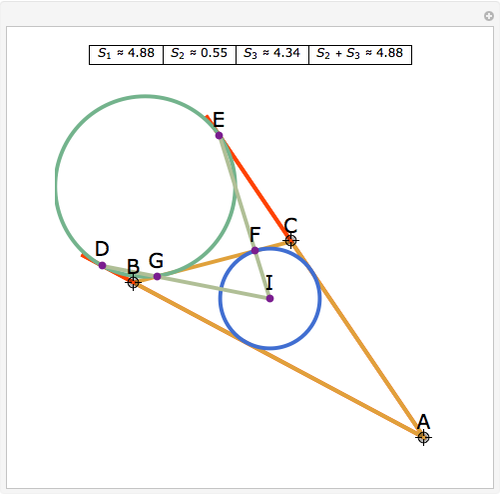
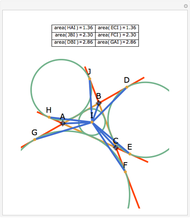
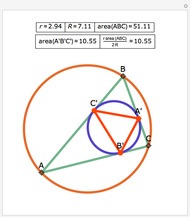
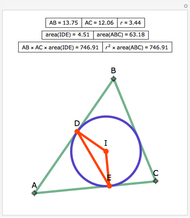
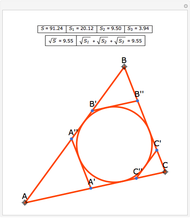
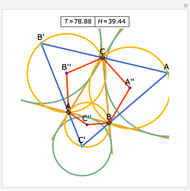
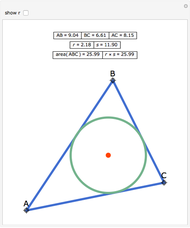
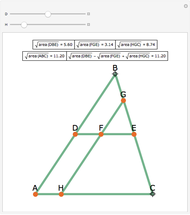
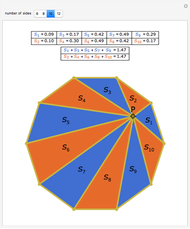
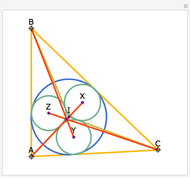
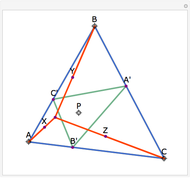
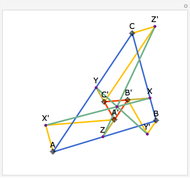
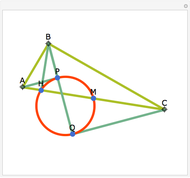
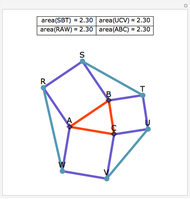
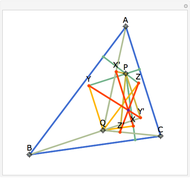
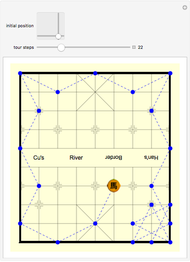
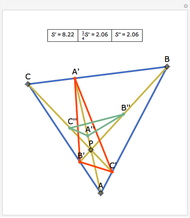
Let ABC be a triangle. Let D and E be the points of contact of the extensions of AB and AC with the excircle opposite A. Let I be the incenter of ABC. let G and F be the intersections of DI and EI with BC. Let 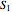, , 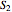and 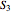be the areas of GIF, DBG, and ECF, respectively. Then .

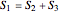Contributed by: Jay Warendorff (March 2011)
After work by: Antonio Gutierrez
Open content licensed under CC BY-NC-SA

Snapshots

Details

The statement of the theorem is in Problem 119. Area of Triangles, Incenter, Excircle.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send