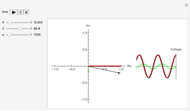
Operational Amplifier Gain-Bandwidth Characteristics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
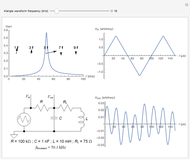
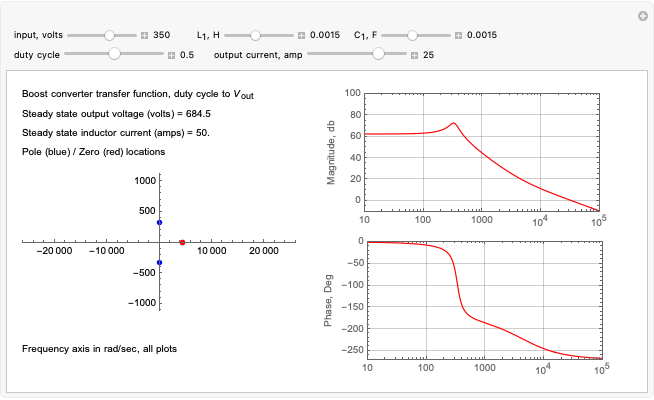
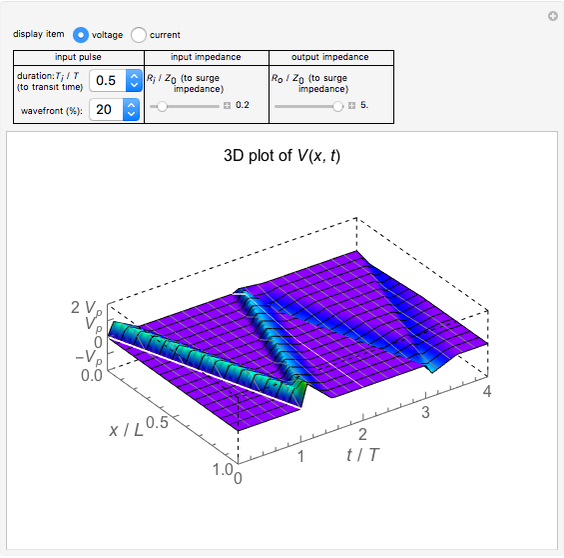
This Demonstration investigates the gain-bandwidth properties of a basic inverting amplifier based on an LM741 operational amplifier. You can toggle the display to show a schematic of the amplifier circuit and a Bode plot displaying its gain-bandwidth properties. This simple amplifier circuit exhibits characteristic roll-off of the gain; that is, the actual gain of the circuit drops below the nominal gain as the frequency of the signal increases. The slew rate describes the time rate of change of the potential at a circuit node.
Contributed by: Michael R. Braunstein (March 2012)
(Central Washington University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
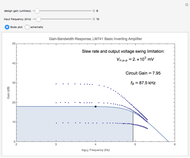
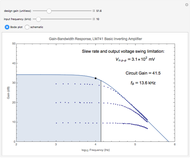
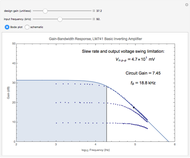
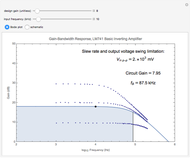
The Bode plot displays the gain in decibels:  on the vertical axis versus the logarithm of the frequency on the horizontal axis. The bandwidth of the amplifier is the range of frequencies for which the circuit gain is within 3 dB of the design gain. The information displayed in the Bode plot includes:
on the vertical axis versus the logarithm of the frequency on the horizontal axis. The bandwidth of the amplifier is the range of frequencies for which the circuit gain is within 3 dB of the design gain. The information displayed in the Bode plot includes:
• a single black point that corresponds to the gain of the circuit for the selected design gain and an input sinusoidal waveform of the selected frequency
• a solid line displaying a model of the entire gain curve of the circuit as a function of frequency, as presented in note A below, for the selected design gain and an input sinusoidal waveform
• a shaded region that represents the bandwidth of the amplifier for the selected design gain
• three dotted lines that show actual data for circuits with design gains of approximately 3, 10, and 30
• a vertical black line that marks the limit of the bandwidth of the amplifier by its intersection with the 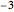 dB roll-off position of the gain curve for the selected design gain
dB roll-off position of the gain curve for the selected design gain
• the gain that the circuit actually delivers with the selected design gain and for a sinusoidal input waveform with the selected frequency and obeying the slew rate and output voltage swing limitations
• the frequency, 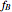 , of the
, of the 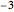 dB roll-off position for the selected design gain
dB roll-off position for the selected design gain
• the maximum peak-to-peak input voltage of a sinusoidal waveform with 0 DC offset that would not be distorted due to the slew rate and output voltage swing limitations of the LM741
Notes
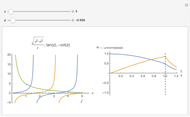
A. Analyses of the basic inverting op-amp amplifier typically assume that it is characterized by a constant gain-bandwidth product. We used a value of 700,000 (V/V) Hz for the gain-bandwidth product of the amplifier based on fitting the three datasets shown in the plot to a gain-frequency relationship of the form
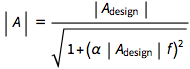 ,
,
where 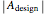 is the design gain of the amplifier,
is the design gain of the amplifier, 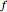 is the frequency of a sinusoidal input waveform, and
is the frequency of a sinusoidal input waveform, and  is a constant.
is a constant.
However, the three values of gain-bandwidth product obtained from the fits actually appeared to be slowly increasing as the design gain increased; that is, our data did not appear to be completely consistent with a constant gain-bandwidth product. This is shown by some systematic disagreement that is evident between the data and the model for both the lowest and highest gain datasets.
B. We based the slew rate limitation on the LM741 data sheet identification of a maximum slew rate of 0.5 V/ sec.
sec.
C. We based the peak-to-peak input voltage limitation on  V power supply and an output voltage swing for an LM741 that is restricted to 1 V less in amplitude than the
V power supply and an output voltage swing for an LM741 that is restricted to 1 V less in amplitude than the 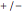 power supply voltages, consistent with the data sheet listed in the references. The data in the plot was collected with a
power supply voltages, consistent with the data sheet listed in the references. The data in the plot was collected with a  V power supply applied to the LM741.
V power supply applied to the LM741.
The author gratefully acknowledges the contribution of Daniel Griffin for the data he collected that is displayed in this Demonstration and that was used as the basis for the gain-bandwidth product applied in calculations.
References
[1] D. Griffin, Data from Exercise 5, Physics 331, Central Washington University. Ellensburg, WA (unpublished, personal communication), 2012.
[2] National Semiconductor, "LM741 Operational Amplifier," Santa Clara, CA: National Semiconductor, 2000. www.ti.com/lit/ds/symlink/lm741.pdf.
[3] R. E. Simpson, Introductory Electronics for Scientists and Engineers, 2nd ed., Englewood Cliffs, NJ: Prentice-Hall, 1987.
Permanent Citation