Details

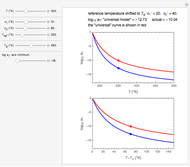
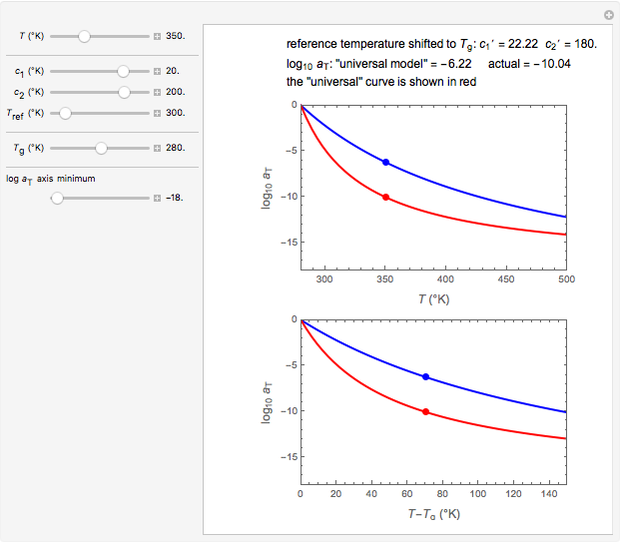
Snapshot 1: versus where and

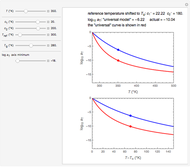
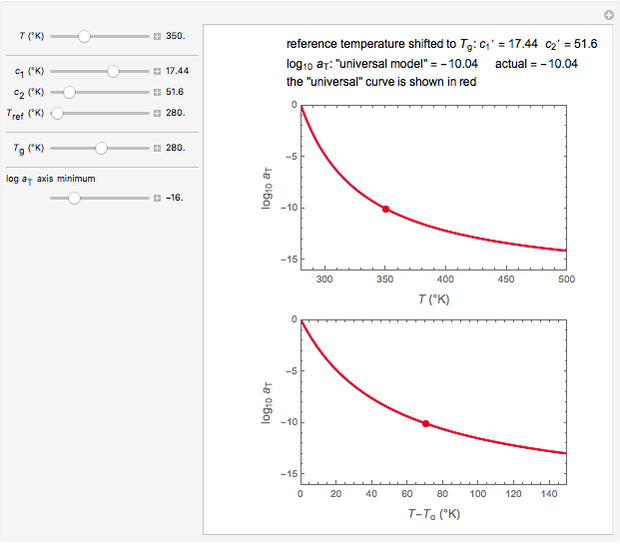
Snapshot 2: versus where and

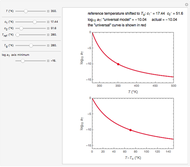
Snapshot 3: versus where and and

The original WLF model can be written as , where is the shift factor, is a reference temperature in °K, and and are experimentally determined constants ( is dimensionless and is in °K). When the arbitrary reference temperature is shifted to the glass transition temperature , the equation becomes , where and , with [1].

The WLF model's authors suggested that in the absence of experimental data one could use and as first approximations. These values were derived by averaging the experimental values of several rubbery polymers and are widely known as the WLF model's universal constants.

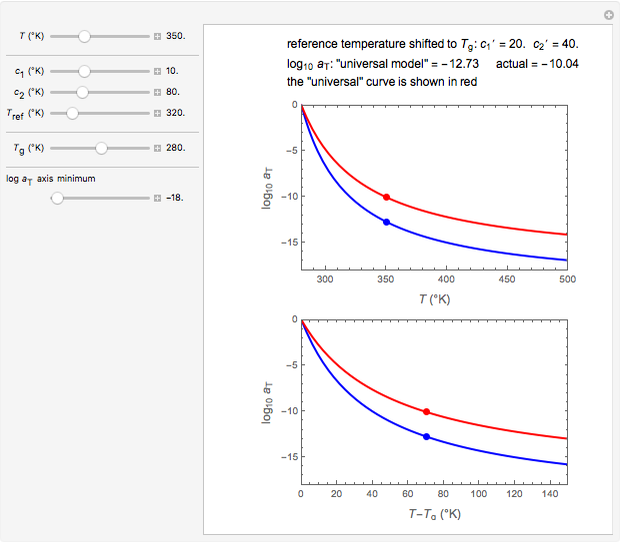
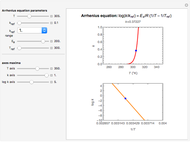
In this Demonstration, experimentally determined constants and , the reference temperature , and the polymers or food's glass transition temperature are entered with sliders. The program then calculates the corresponding and and displays, on the same graph, the resulting versus relationship superimposed on that produced with the universal constants. The two curves, together with the calculated values of and , are presented in the forms of versus (top) and versus (bottom) whose ranges can also be selected with sliders. Notice that even for the same polymer, the observed glass transition temperature can vary dramatically depending on the method of its determination, the test's conditions, and the heating or cooling rate [2, 3].

Note that not all combinations of slider-entered values describe a realistic versus relationship. When this occurs, all panel output is replaced by the message "unrealistic entries".

References

[1] M. Peleg, "On the Use of the WLF Model in Polymers and Foods," Critical Reviews in Food Science and Nutrition, 32(1), 1992 pp. 59–66. doi:10.1080/10408399209527580.

[2] R. J. Seyler, ed., Assignment of the Glass Transition, Philadelphia: American Society of Testing Materials, 1994.

[3] E. Donth, The Glass Transition: Relaxation Dynamics in Liquids and Disordered Materials, Berlin: Springer–Verlag, 2001.