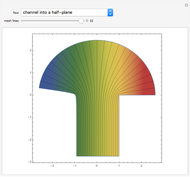
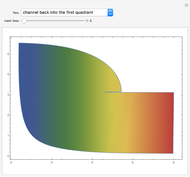
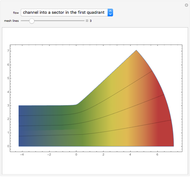
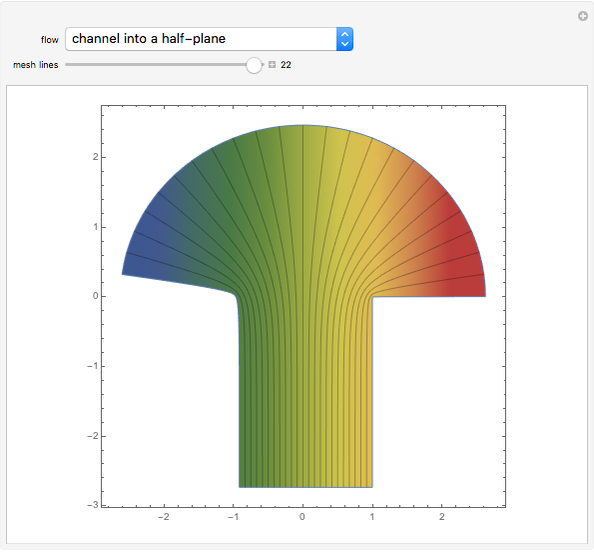
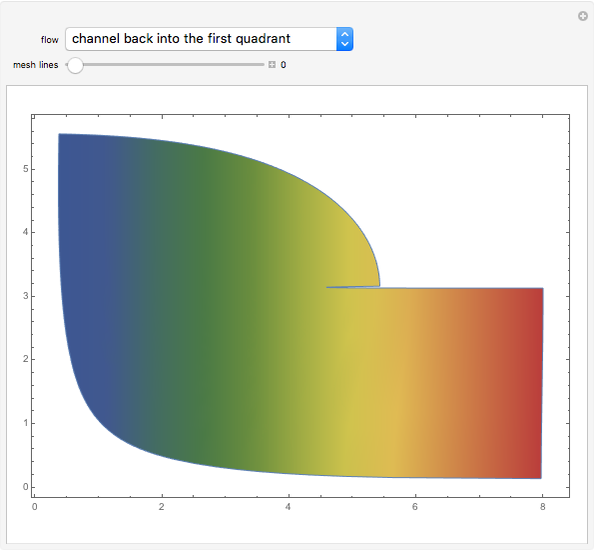
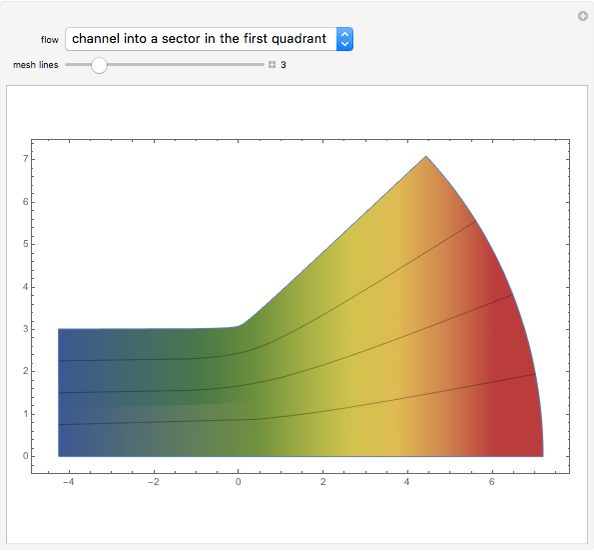
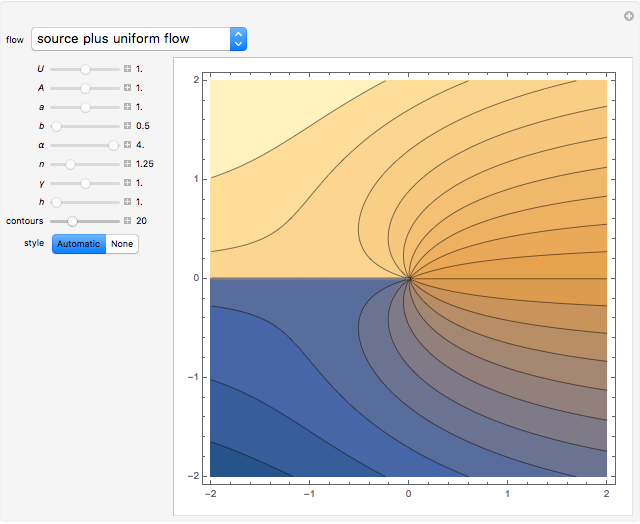
Potential Flows through Channels

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
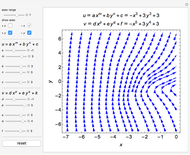
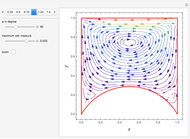
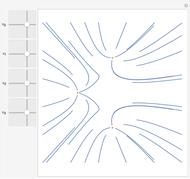
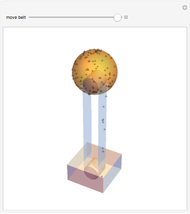
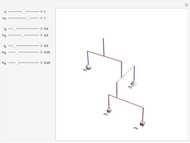
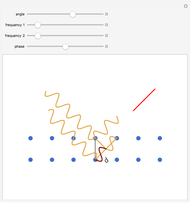
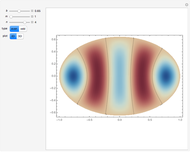
Potential flows describe the velocity field as the gradient of a scalar function: the velocity potential. This is a solution of Laplace's equation for the case of an irrotational velocity field. In this Demonstration, the flows go from a channel to another region with several choices of geometries. We apply the Schwarz–Christoffel transformation, which conformally maps the upper half-plane onto the interior of a polygon.
Contributed by: Enrique Zeleny (October 2014)
Open content licensed under CC BY-NC-SA
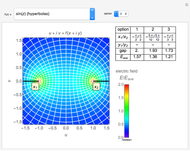
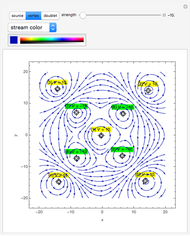
Snapshots
Details
Reference
[1] J. H. Mathews and R. W. Howell, Complex Analysis: For Mathematics and Engineering, 6th ed., Sudbury, MA: Jones & Bartlett Learning, 2012 pp. 435–522. mathfaculty.fullerton.edu/mathews/complex.html.
Permanent Citation