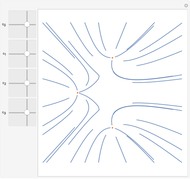
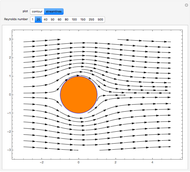
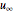Velocity Stream Lines from Superposition of Elementary Fluid Flows

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
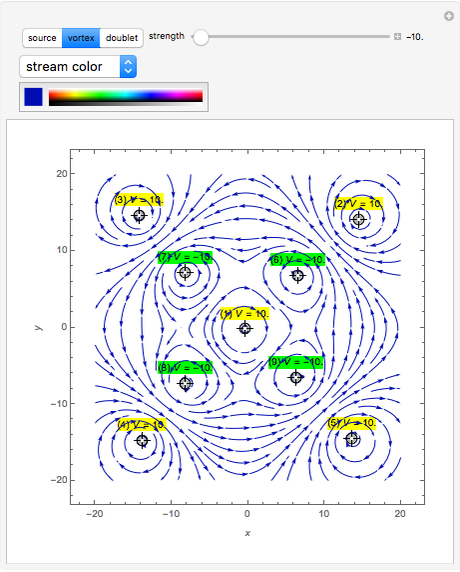
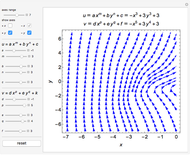
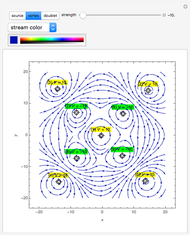
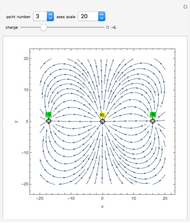
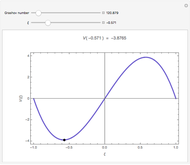
Initially there is one locator that represents source flow at the origin, labeled "(1)  = 1". The first 1 is the current number of the locator. The symbol
= 1". The first 1 is the current number of the locator. The symbol  ,
,  , or
, or  is an abbreviation for source, vortex, or doublet, respectively. The last 1 is the value of the slider "strength". Positive and negative strengths appear with yellow and green backgrounds, respectively.
is an abbreviation for source, vortex, or doublet, respectively. The last 1 is the value of the slider "strength". Positive and negative strengths appear with yellow and green backgrounds, respectively.
Contributed by: Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The stream functions for source, vortex, and doublet elementary flows are  ,
, 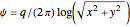 , and
, and  , respectively, where
, respectively, where  is a measure of the strength of the flows.
is a measure of the strength of the flows.
The velocities are obtained from 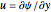 and
and 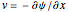 . Next
. Next  and
and 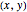 are replaced by
are replaced by  and
and  to obtain the velocity at
to obtain the velocity at  with strength
with strength  as follows.
as follows.
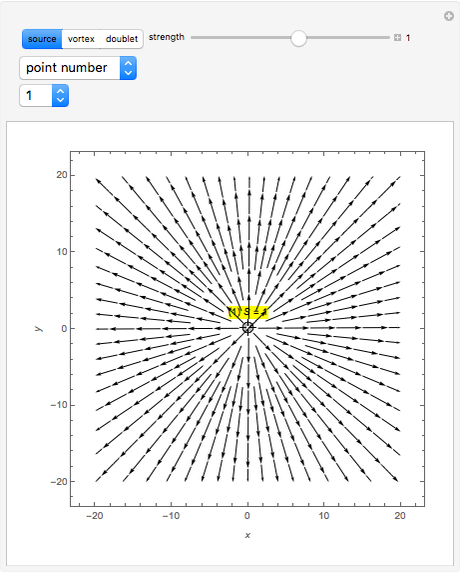
The source flow  , from the point) or sink flow (
, from the point) or sink flow (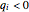 , to the point):
, to the point):


Vortex flow  , clockwise rotating) or
, clockwise rotating) or  , counterclockwise rotating):
, counterclockwise rotating):
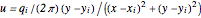
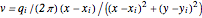
Doublet flow  , left through the point) or
, left through the point) or  , right through the point):
, right through the point):
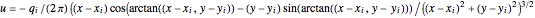
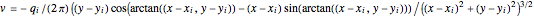
Uniform flow:
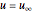

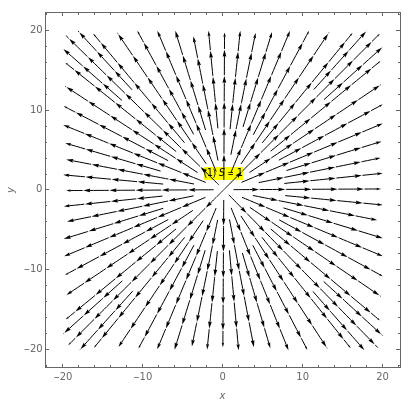
This uniform flow is equivalent to the flow with velocity 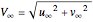 in the direction
in the direction  .
.
The velocity field stream lines are plotted by using superposition of the above velocities with strength  located at the points
located at the points  .
.
It is interesting to compare this Demonstration with the applet given in the related links. The results are similar but the vortex positive rotation here is clockwise, while there it is counterclockwise.
See the applet on the superposition of elementary flows.
Permanent Citation