Potential of a Charged Spheroid

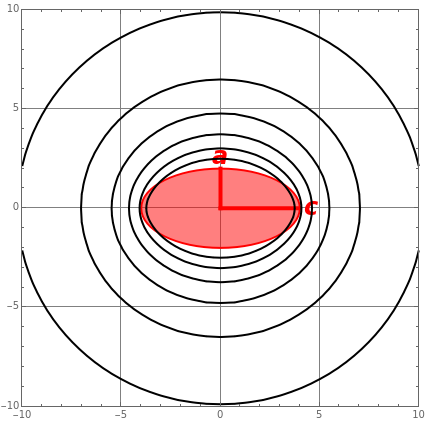
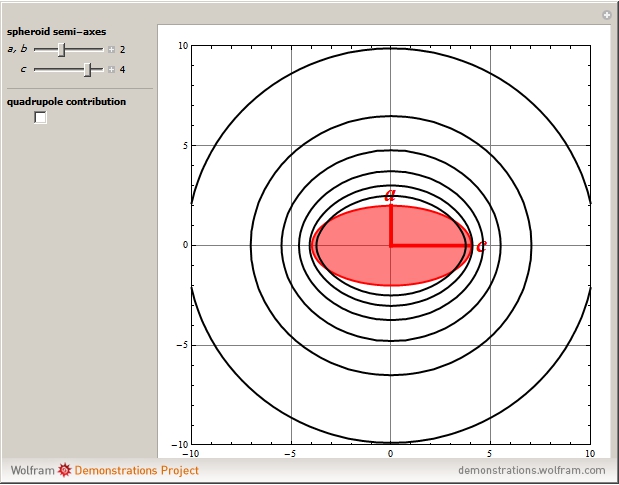
This Demonstration shows the electrostatic potential of a uniformly charged spheroid. We consider both prolate spheroids, with , and oblate spheroids, with . Here , , are the semi-axes, with the axis oriented horizontally. The potential is cylindrically symmetrical and it suffices to show just the plane containing the axis. The potential external to the spheroid is given by , the sum representing a multipole expansion over the charge distribution. For an oblate or prolate spheroid, the monopole contribution is dominant, with only the quadrupole term making a significant additional contribution to the potential. The quadrupole moment of a charged spheroid is given by .

You can select the semi-axes and to display a scaled contour plot of the potential. Multiply by to find the actual potential. The same result pertains to a gravitational potential, with as the scaling factor. You can isolate the quadrupole contribution with the checkbox.