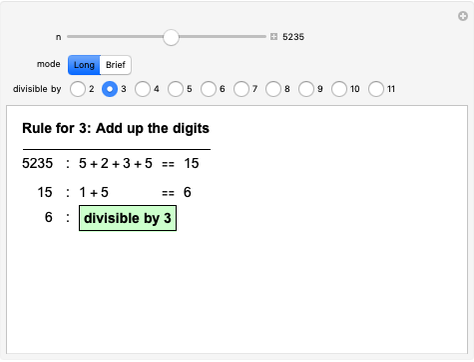
MIU Explorer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
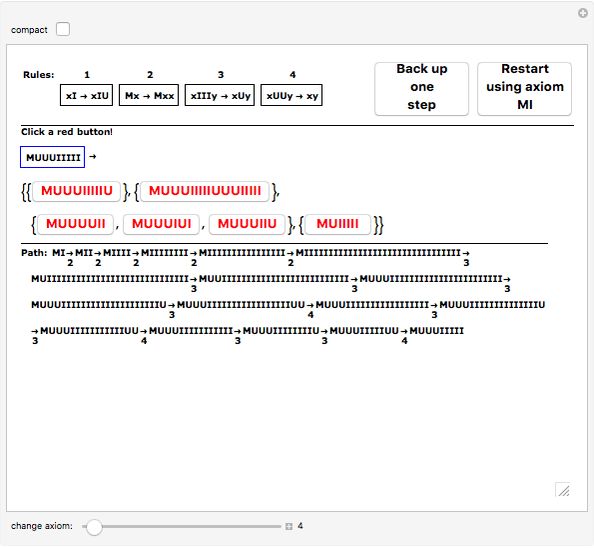
Explore the MIU-system [1] by clicking the red buttons, each of which represents the creation of a new theorem of the system by applying a rule of inference to a previously found theorem. The main features of the display are (a) the list of rules for your reference; (b) the current theorem (framed in blue); and (c) the options possible by applying all rules in all possible ways, given as a list of four lists of red buttons.
[more]
Contributed by: Ken Caviness (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration lets you explore the MIU-system and the MU-puzzle [1], an example formal system and accompanying challenge introduced by Douglas Hofstadter in Chapter 1 of Gödel, Escher, Bach as a means of illustrating the important elements of formal systems (axioms, theorems, rules of inference), the mechanical and intelligent modes of treating a formal system, and the concept of a decision procedure. The four rules of inference of the system are shown. The MU-puzzle is to start with the axiom 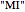 and derive (or generate, or prove)
and derive (or generate, or prove) 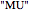 . Rather than simply generating all possible theorems [2], at each step all choices are displayed and you are invited to pick a path to follow by clicking one of the buttons shown in the main window. The growing path (the current theorem's proof) is also displayed. This removes much of the drudgery of the
. Rather than simply generating all possible theorems [2], at each step all choices are displayed and you are invited to pick a path to follow by clicking one of the buttons shown in the main window. The growing path (the current theorem's proof) is also displayed. This removes much of the drudgery of the 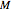 -mode for solving the puzzle, and frees the human researcher to more easily make the jump to
-mode for solving the puzzle, and frees the human researcher to more easily make the jump to 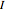 -mode (i.e., to jump outside the system and think about it).
-mode (i.e., to jump outside the system and think about it).
Possible theorems of the system consist of strings of the letters 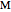 ,
, 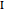 ,
, 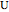 . Only one theorem is given at the start: the axiom. Other theorems must be generated by applying the rules to the axiom (or any other already-generated theorem). The
. Only one theorem is given at the start: the axiom. Other theorems must be generated by applying the rules to the axiom (or any other already-generated theorem). The  and
and 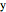 in the rules can stand for any valid substrings (including the length 0 string).
in the rules can stand for any valid substrings (including the length 0 string).
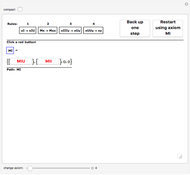
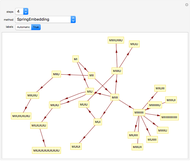
Snapshot 1: starting point for the MU-puzzle. Only the axiom "MI" is given, but either rule 1 or rule 2 can be applied at this point. If rule 1 (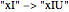 ) is applied with the
) is applied with the  standing for
standing for 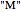 , we have
, we have  . The application of rule 2 (
. The application of rule 2 ( ) with
) with  representing
representing 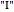 gives
gives 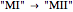 . The empty lists for rules 3 and 4 indicate that they cannot be applied at this point: the patterns do not match.
. The empty lists for rules 3 and 4 indicate that they cannot be applied at this point: the patterns do not match.
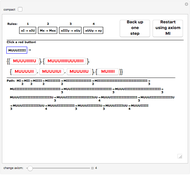
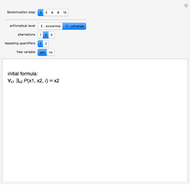
Snapshot 2: a situation in which any of the rules could be applied. In the case of rule 3 (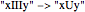 ), depending on the choice of
), depending on the choice of 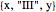 , the match can occur in three ways:
, the match can occur in three ways: 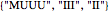 ,
, 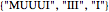 , or
, or 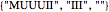 , resulting in
, resulting in 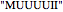 ,
, 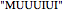 , or
, or 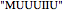 , respectively. The match for rule 4 (
, respectively. The match for rule 4 (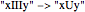 ) can also occur in multiple ways with
) can also occur in multiple ways with 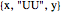 :
: 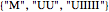 or
or 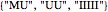 , but since the result will be
, but since the result will be 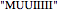 in either case, the duplicate case is not shown.
in either case, the duplicate case is not shown.
If the path becomes too long or its continuation is obvious, the "back up" button can be used to return to a more interesting branch. (But note that the MIU-system does not allow reversing the direction of theorem generation, so in backtracking we are reverting to an earlier position on the path, not "moving backwards".) The restart button can be used to simply start over from the axiom.
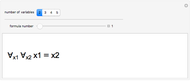
Snapshot 3: the same situation shown in compact display mode, using exponents to shorten the strings shown. For example, 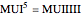 and
and 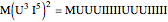 .
.
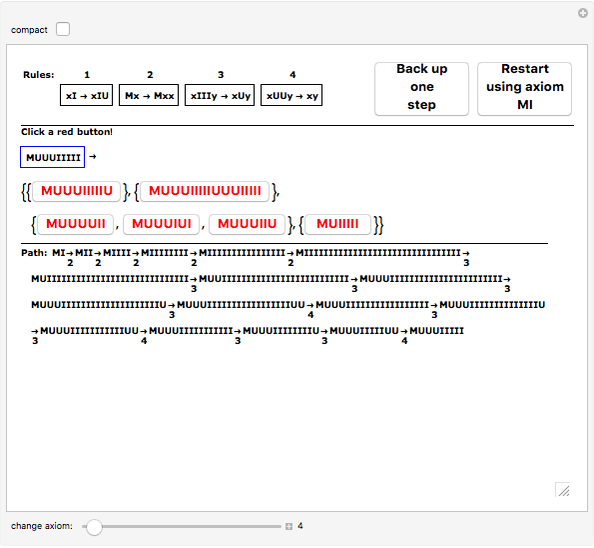
Snapshot 4: going beyond the MU-puzzle. Adjusting the slider and then clicking the restart button lets you explore other regions of the MIU-system, starting with alternative axioms, but for many axioms (such as the one shown here,  ) none of the rules can be applied and no additional theorems can be generated.
) none of the rules can be applied and no additional theorems can be generated.
References:
[1] Douglas R. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, New York: Basic Books, 1979.
[2] For an example of this, see "Hofstadter's MU Riddle" in the Related Links section below.
Permanent Citation