Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Hofstadter's MU Riddle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

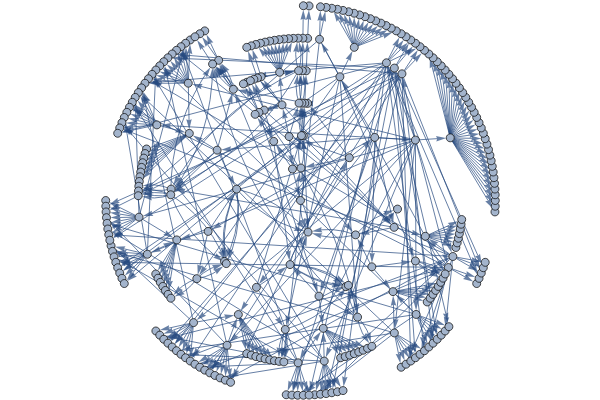
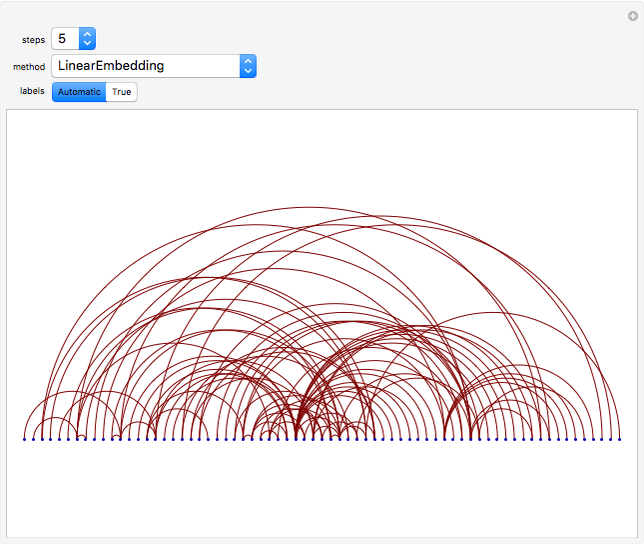
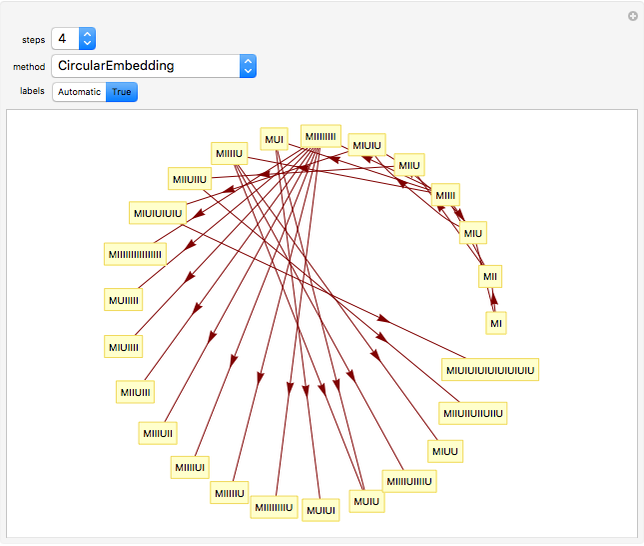
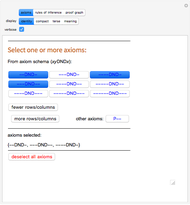
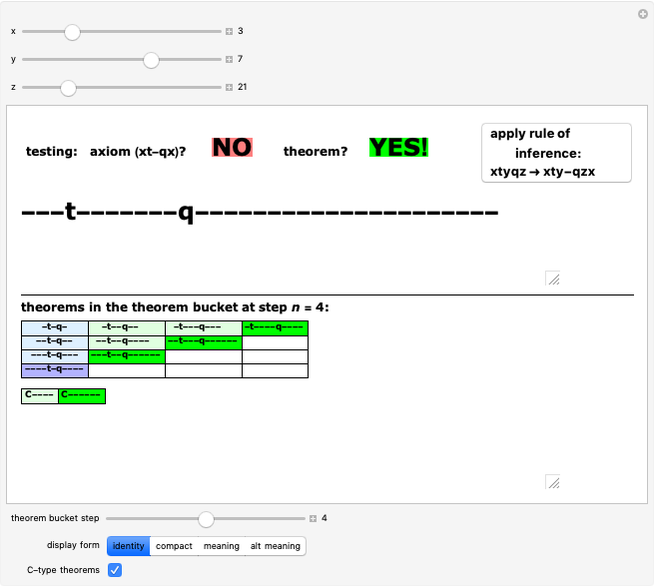
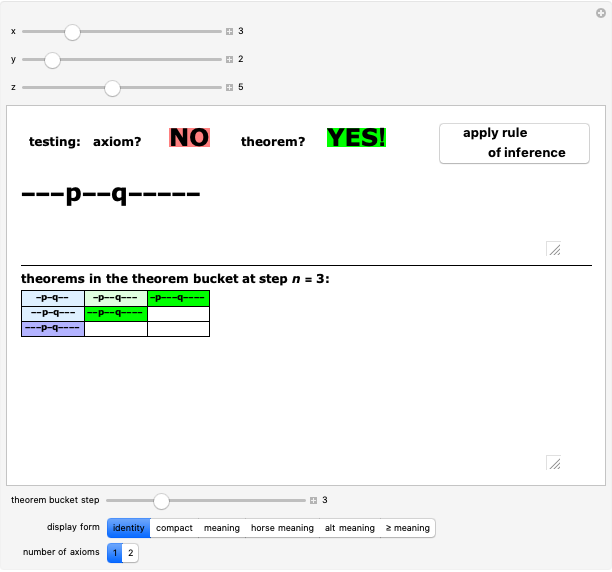
Originally proposed by Douglas Hofstadter in his seminal work Gödel, Escher, Bach: An Eternal Golden Braid, the MU-Puzzle describes a formal system with a single axiom and four rules used to generate new theorems, written as sequences over the alphabet {M,I,U}, from the axiom MI by repeated application of the following rules:

[more]

1. If a string ends in I, you may append a U onto the end. 2. If a string is of the form Mx, you may rewrite it to Mxx. 3. If the string contains III, you may replace those letters with U. 4. If the string contains UU, you may remove those letters.

The puzzle is to answer the following question: is MU a theorem of the system?

[less]

Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send