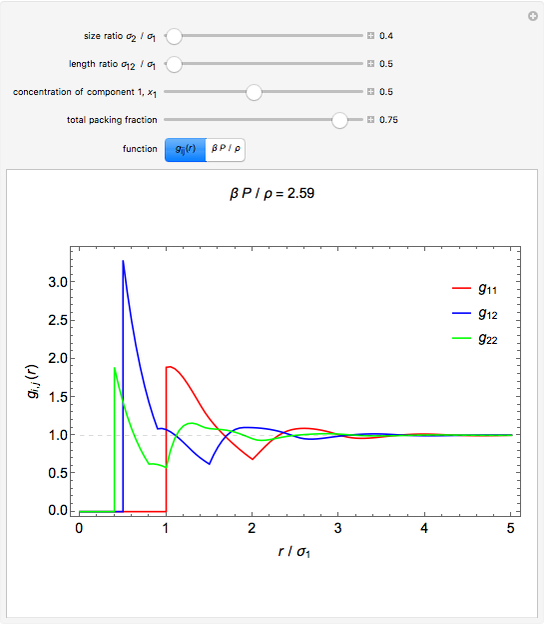
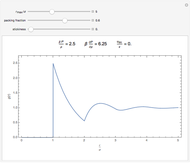
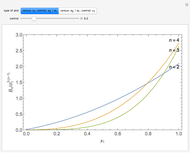
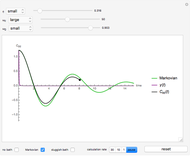
Radial Distribution Functions for Nonadditive Hard-Rod Mixtures

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
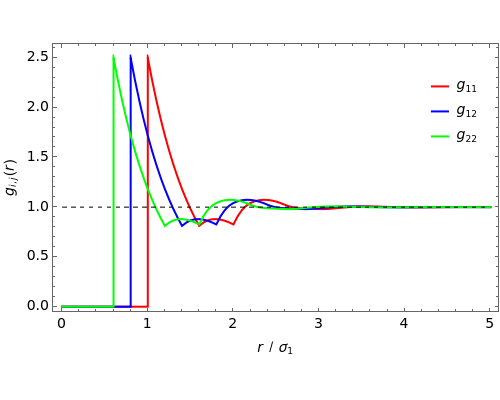
In statistical mechanics, the radial distribution function represents the distribution of interparticle separations [1]. This Demonstration shows the results of exact statistical-mechanical computations of the radial distribution functions  for a one-dimensional binary system of particles interacting via hard-rod potentials [2, 3].
for a one-dimensional binary system of particles interacting via hard-rod potentials [2, 3].
Contributed by: Andrés Santos (June 2015)
Open content licensed under CC BY-NC-SA
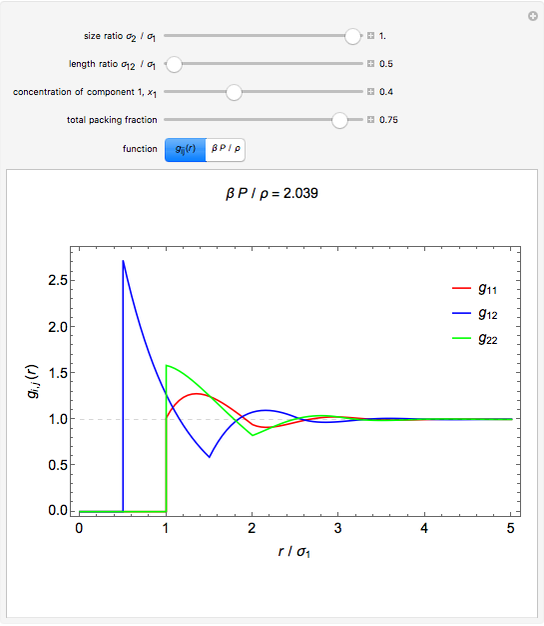
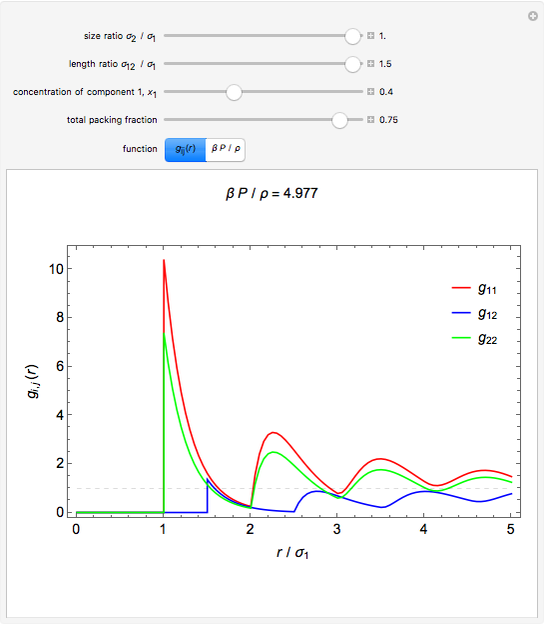
Snapshots
Details
References
[1] Wikipedia. "Radial Distribution Function." (Jun 8, 2015) en.wikipedia.org/wiki/Radial_distribution_function.
[2] Z. W. Salsburg, R. W. Zwanzig, and J. G. Kirkwood, "Molecular Distribution Functions in a One-Dimensional Fluid," The Journal of Chemical Physics, 21(6), 1953 pp. 1098–1107. doi:10.1063/1.1699116.
[3] A. Santos, "Exact Bulk Correlation Functions in One-Dimensional Nonadditive Hard-Core Mixtures," Physical Review E, 76(6), 2007 062201. doi:10.1103/PhysRevE.76.062201.
Permanent Citation