Radial Distribution Function for One-Dimensional Triangle Well and Ramp Fluids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
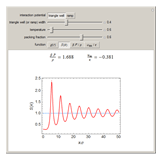
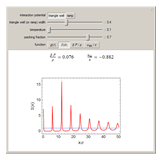
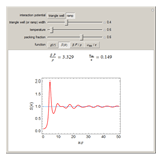
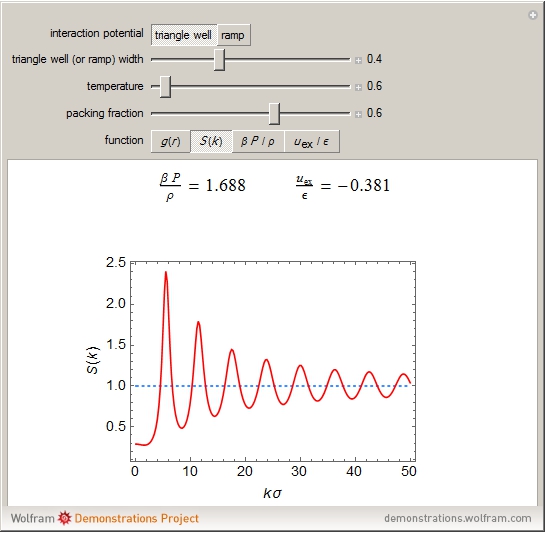
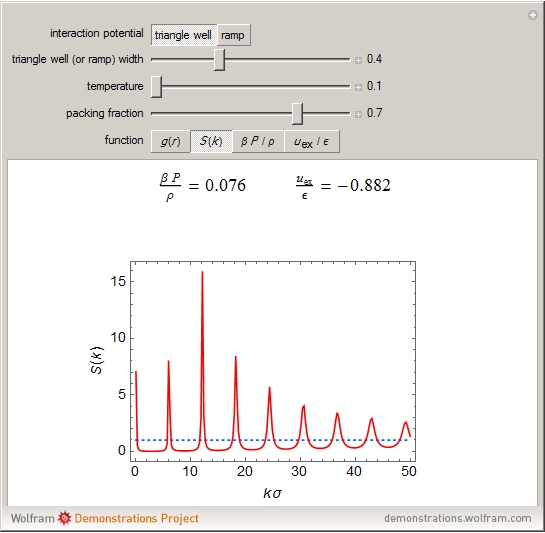
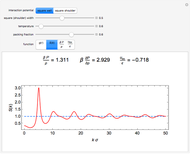
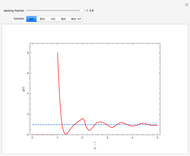
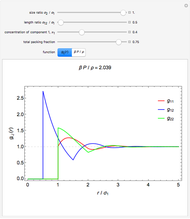
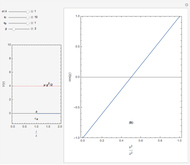
In statistical mechanics, the radial distribution function describes how density varies as a function of distance from a reference particle [1]. This Demonstration shows the results of exact statistical-mechanical computations of the radial distribution function 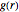 and the structure factor
and the structure factor 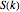 [2] for a one-dimensional system of particles interacting via triangle well or ramp potentials [3–5]. We also find the values of the ratio
[2] for a one-dimensional system of particles interacting via triangle well or ramp potentials [3–5]. We also find the values of the ratio  (where
(where  is the inverse temperature,
is the inverse temperature,  is the pressure and
is the pressure and  is the number density) and the excess internal energy per particle
is the number density) and the excess internal energy per particle  . The sliders allow you to control the width of the triangle well or ramp, the reduced temperature and the packing fraction. The quantities
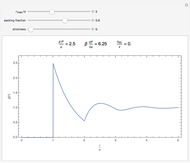
. The sliders allow you to control the width of the triangle well or ramp, the reduced temperature and the packing fraction. The quantities  and
and  are also plotted as functions of the packing fraction.
are also plotted as functions of the packing fraction.
Contributed by: Ana M. Montero and Andrés Santos (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this one-dimensional system, the particles interact with an impenetrable hard core of length  plus either an attractive triangle well or a repulsive ramp potential of energy
plus either an attractive triangle well or a repulsive ramp potential of energy  and width
and width  . This can be represented by a pairwise potential energy function
. This can be represented by a pairwise potential energy function 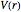 . The exact solution for the radial distribution function
. The exact solution for the radial distribution function 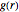 is worked out in [3–5]. As a very rudimentary approximation,
is worked out in [3–5]. As a very rudimentary approximation, 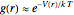 . The structure factor is given by
. The structure factor is given by  .
.
References
[1] Wikipedia. "Radial Distribution Function." (Apr 11, 2018) en.wikipedia.org/wiki/Radial_distribution_function.
[2] Wikipedia. "Structure Factor." (Apr 11, 2018) en.wikipedia.org/wiki/Structure_factor.
[3] Z. W. Salsburg, R. W. Zwanzig and J. G. Kirkwood, "Molecular Distribution Functions in a One-Dimensional Fluid," The Journal of Chemical Physics, 21(6), 1953 pp. 1098–1107. doi:10.1063/1.1699116.
[4] A. Santos, A Concise Course on the Theory of Classical Liquids: Basics and Selected Topics, Switzerland: Springer International Publishing, 2016. link.springer.com/978-3-319-29668-5.
[5] A. M. Montero, "Correlation Functions and Thermophysical Properties of One-Dimensional Liquids." arxiv.org/abs/1710.01118.
Permanent Citation