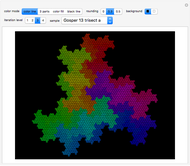
Fractal Ir-rep-tiles of Order Two

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
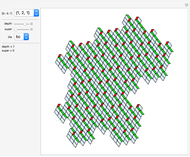
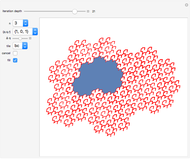
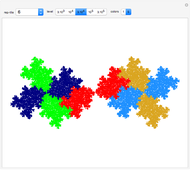
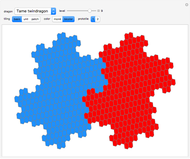
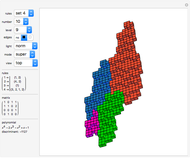
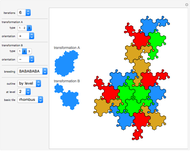
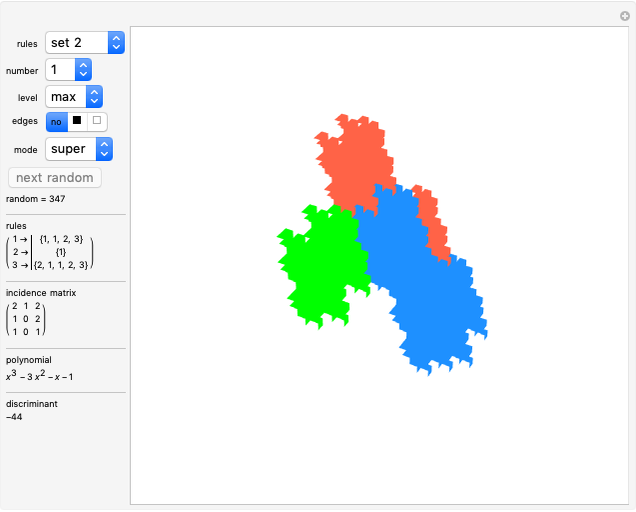
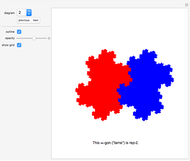
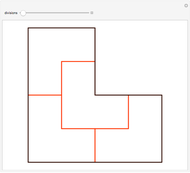
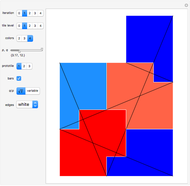
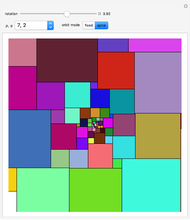
This Demonstration shows nine ir-rep-tiles of order two with fractal boundary using the iterated function system (IFS) chaos game method.
Contributed by: Dieter Steemann (February 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A shape that can be tiled with smaller congruent copies of itself is called a rep-tile [1]. If the tiling uses  copies, the shape is said to be of order
copies, the shape is said to be of order  . A shape that tiles itself using copies of different sizes is called an irregular rep-tile or ir-rep-tile. This Demonstration is limited to ir-rep-tiles of order two with compact disk-like shape and fractal boundary. Only a few such ir-rep-tiles are known. Hinsley [2] has listed seven such ir-rep-tiles of order two. Here, nine such ir-rep-tiles are shown.
. A shape that tiles itself using copies of different sizes is called an irregular rep-tile or ir-rep-tile. This Demonstration is limited to ir-rep-tiles of order two with compact disk-like shape and fractal boundary. Only a few such ir-rep-tiles are known. Hinsley [2] has listed seven such ir-rep-tiles of order two. Here, nine such ir-rep-tiles are shown.
All examples are related to roots of the polynomial  with
with  . Approximations of the fractal tilings are produced by an iterated function system (IFS) using the chaos game method. Example 2 is the well-known Hokkaido tiling, named by Shigeki Akiyama in reference to the Japanese island with the same name.
. Approximations of the fractal tilings are produced by an iterated function system (IFS) using the chaos game method. Example 2 is the well-known Hokkaido tiling, named by Shigeki Akiyama in reference to the Japanese island with the same name.
References
[1] Wikipedia. "Rep-tile." (Feb 14, 2018) en.wikipedia.org/wiki/Rep-tile.
[2] S. Hinsley. "2 Element Ir-Rep-tiles." (Feb 14, 2018) web.archive.org/web/20111212001755/http://www.meden.demon.co.uk/Fractals/dimerIRR.html.
Permanent Citation