Relativistic Addition of Velocities

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
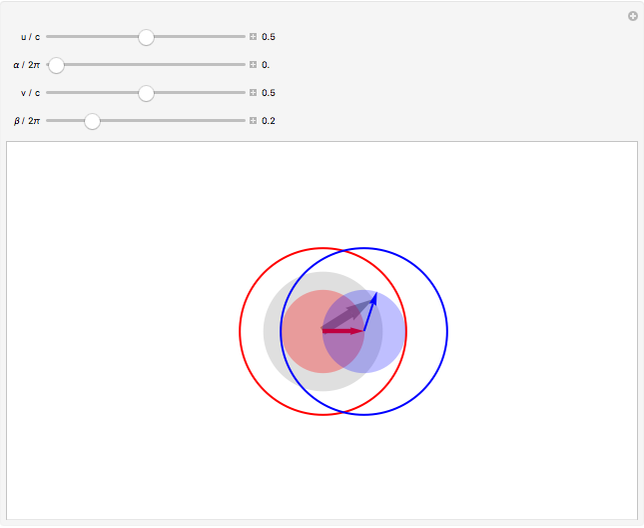
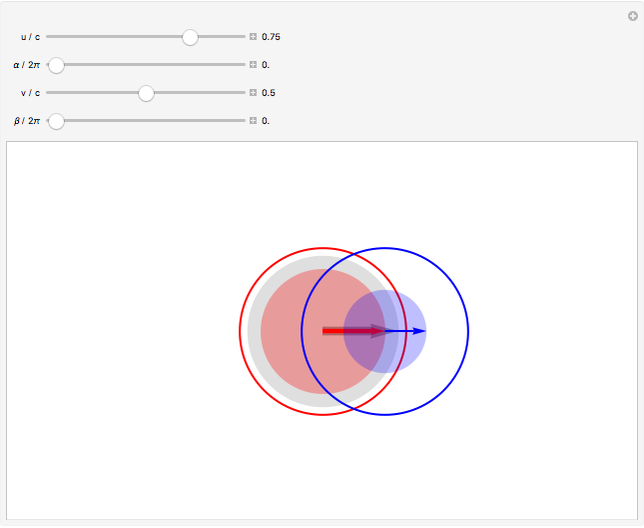
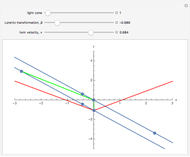
This Demonstration considers the composition of velocities in accordance with the special theory of relativity. Consider a system moving with velocity represented by the red arrow, with magnitude  and direction
and direction  , with respect to a stationary frame of reference. The red disk recapitulates this magnitude, which has an upper limit extending to the red circle, corresponding to the speed of light
, with respect to a stationary frame of reference. The red disk recapitulates this magnitude, which has an upper limit extending to the red circle, corresponding to the speed of light  . The blue arrow represents a second velocity, which has a magnitude
. The blue arrow represents a second velocity, which has a magnitude  and direction
and direction 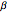 , with respect to the moving frame of reference. The velocity with respect to the original stationary frame is then represented by
, with respect to the moving frame of reference. The velocity with respect to the original stationary frame is then represented by 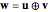 . A compact formulation gives the components of
. A compact formulation gives the components of  parallel and perpendicular to
parallel and perpendicular to  :
: 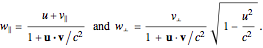 The gray arrow represents the vector
The gray arrow represents the vector  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
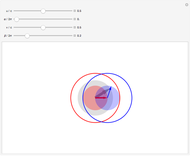
Snapshot 1: for  , the Galilean result
, the Galilean result  is a good approximation
is a good approximation
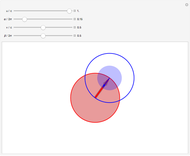
Snapshot 2: if  or
or  , then
, then 
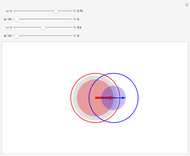
Snapshot 3: the collinear case reduces to Einstein's well-known formula 
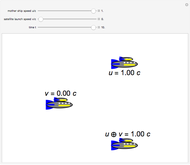
Snapshots 4, 5: velocity addition is not commutative; 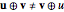
Reference: J. D. Jackson, Classical Electrodynamics, 3rd ed., New York: John Wiley & Sons, 1998 p. 531.
Permanent Citation