Risk Regulation Relying on Historical Standard Deviation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
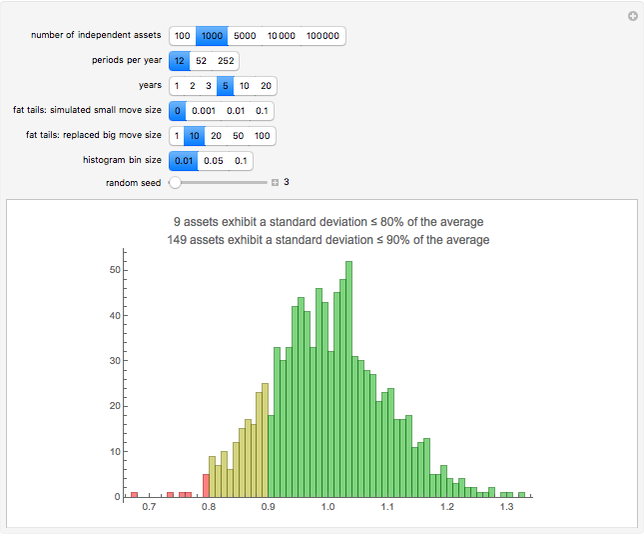
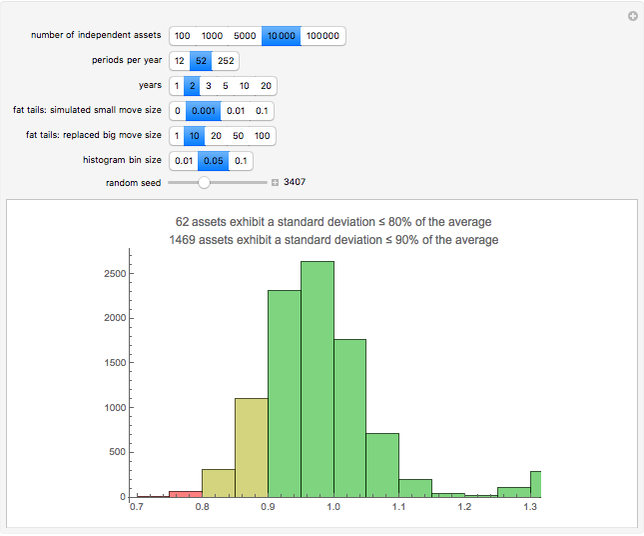
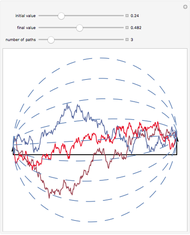
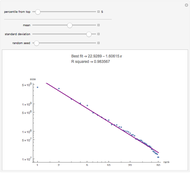
Given a number of assets assumed to be independent, the number of periods per year (daily, weekly, or monthly), and the number of years, a simulation of normal returns is run and the historical standard deviation computed for each asset. Those with standard deviations below 80% or 90% of the average are highlighted, indicating assets that would appear to be less risky under any risk regulation schema that is proportional to historical standard deviation, such as parametric value-at-risk commonly allowed by Basel regulations. The fat tail parameters allow the simulation of a distribution with higher kurtosis by replacing draws near zero with more extreme values.
Contributed by: Philip Z. Maymin and Zakhar G. Maymin (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
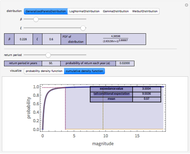
When the periods per year and the number of years are relatively low compared with the impact and probability of a fat tail event, the distribution of standard deviations relative to the return appears punctuated. For example, for 10 years of monthly returns with fat tails simulated by replacing moves less than 0.1 with moves of the same sign of magnitude 10, there appear about a dozen punctuated points with noise around them rather than a single seeming distribution. This is because the jumps are so large, and so infrequent, that one can essentially gather the results based on the number of jumps that have occurred. In such situations, it is better to look either at daily returns or at longer durations, or both, to get a more continuous and unified distribution. The result is that the noise from fat tails essentially offsets the gains to precision from looking at daily returns.
For more information, see P. Z. Maymin and Z. G. Maymin, "Any Regulation of Risk Increases Risk," available at ssrn.com/abstract=1587043.
Permanent Citation
"Risk Regulation Relying on Historical Standard Deviation"
http://demonstrations.wolfram.com/RiskRegulationRelyingOnHistoricalStandardDeviation/
Wolfram Demonstrations Project
Published: November 21 2011