The Normal Inverse Gaussian Lévy Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
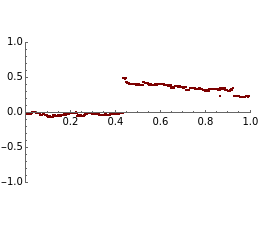
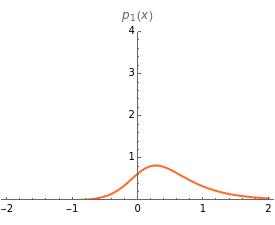
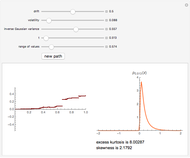
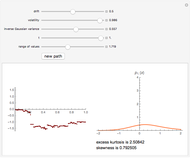
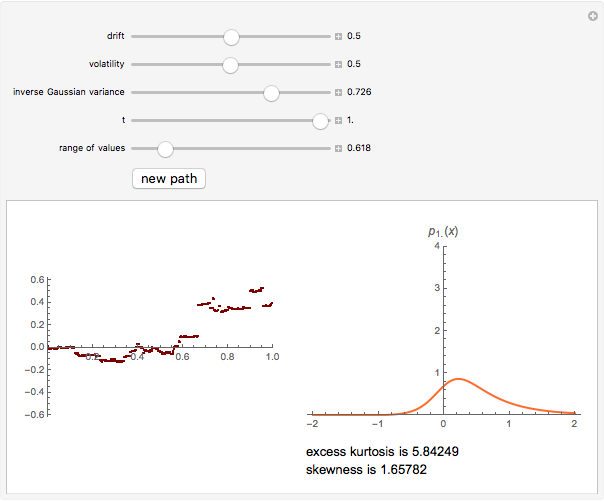
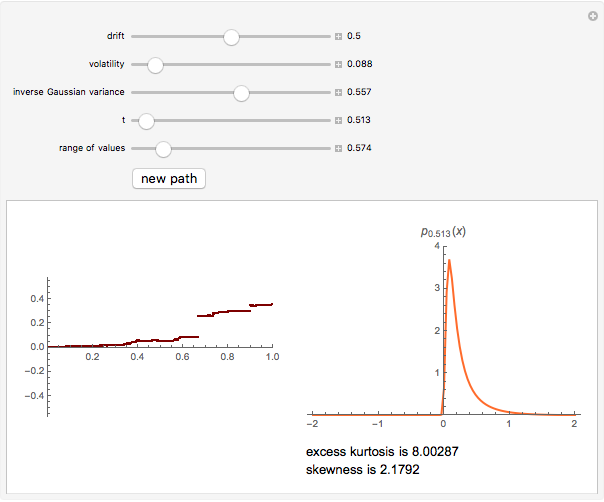
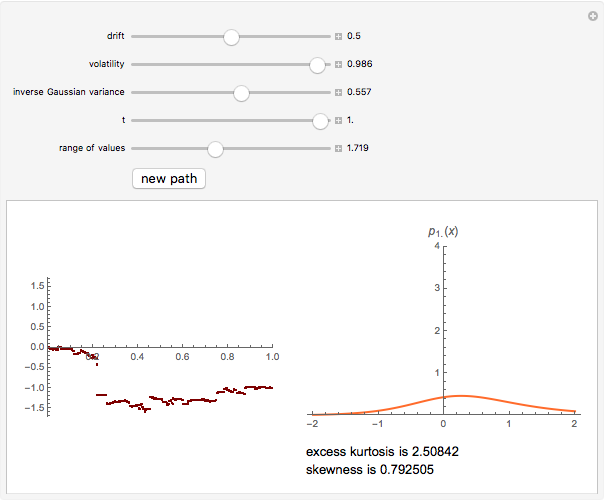
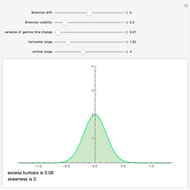
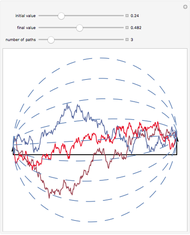
This Demonstration shows a path of the normal inverse Gaussian (NIG) Lévy process and the graph of the probability density of the process at various moments in time. The NIG process is a pure-jump Lévy process with infinite variation, which has been used successfully in modeling the distribution of stock returns on the German and Danish exchanges. The version of the model shown here is controlled by three parameters that arise from the realization of the process as a time-changed Brownian motion with drift. The parameters are the drift and the volatility of the Brownian process and the variance of the (inverse Gaussian) subordinator (whose expectation is assumed to be 1). In the limiting case when the variance of the subordinator is set to zero, the NIG process coincides with Brownian motion and the probability density is normal. For other values of the variance, the NIG probability density has nonzero excess kurtosis and skewness, displayed beneath the graph on the right.
[more]
Contributed by: Piotr Teklinski, Piotr Wroblewski, and Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The normal inverse Gaussian distribution and associated stochastic processes were introduced by Barndorff-Nielsen in [1] and [2]. The name derives from its representation as the distribution of Brownian motion with drift time changed by the inverse Gaussian Lévy process. Since the distribution is infinitely divisible, it gives rise to a corresponding Lévy process, which has been shown capable of accurately modelling the returns on a number of assets on German, Danish, and U.S. exchanges [4].
The normal inverse Gaussian Lévy process is in many ways similar to the variance gamma process due to Madan and Seneta. Both belong to the family of Lévy processes of the generalized hyperbolic type; however, they possess unique properties that make them particularly tractable and convenient for option pricing. In particular, they are alone in the hyperbolic family as having the property of being closed under convolution (i.e., the sum of independently distributed variables of the given type has the same type). Both processes can be represented as a time change of a Brownian motion with drift by a Lévy process with increasing increments. In the case of the variance gamma process the time change process is the gamma process; in the case of a NIG process it is an inverse gamma process. Both processes are pure-jump Lévy processes (they have no continuous Brownian component), but they differ in the nature of jumps: the variance gamma process has jumps of finite variation while the variation of the NIG process is infinite.
There are several common parametrizations of the NIG process. Most of them use four parameters. Here, however, we use a three-parameter representation given in [4]. The parameters are the drift and volatility of the time-changed Brownian process and the variance of the time-change process, which is assumed to have expectation 1. (This does not lose generality due to the scaling properties of the NIG process). This representation brings out clearly the similarity between the NIG process and the variance gamma process; in particular, when the variance of the time change tends to 0 both processes approximate the Brownian motion process.
References:
[1] O. E. Barndorff–Nielssen, "Normal Inverse Gaussian Distributions and Stochastic Volatility Modelling," Scandinavian Journal of Statistics, 24, 1997 pp. 1–13.
[2] O. E. Barndorff–Nielssen, "Processes of Normal Inverse Gaussian Type," Finance and Stochastics, 2(1), 1998 pp. 41–68.
[3] R. Cont and P. Tankov, Financial Modelling with Jump Processes, Boca Raton, FL: CRC Press, 2004.
[4] T. H. Rydberg, "The Normal Inverse Gaussian Lévy Process: Simulation and Approximation", Comm. Stat.: Stoch. Models, 13(4), 1997 pp. 887–910.
Permanent Citation
"The Normal Inverse Gaussian Lévy Process"
http://demonstrations.wolfram.com/TheNormalInverseGaussianLevyProcess/
Wolfram Demonstrations Project
Published: March 7 2011