Two Jump Diffusion Processes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
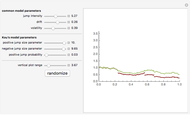
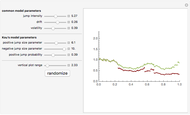
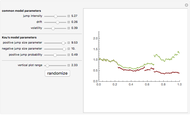
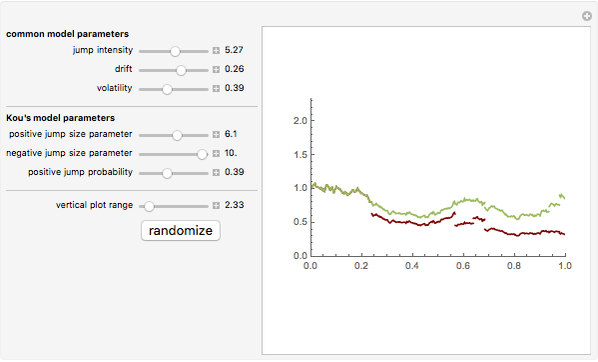
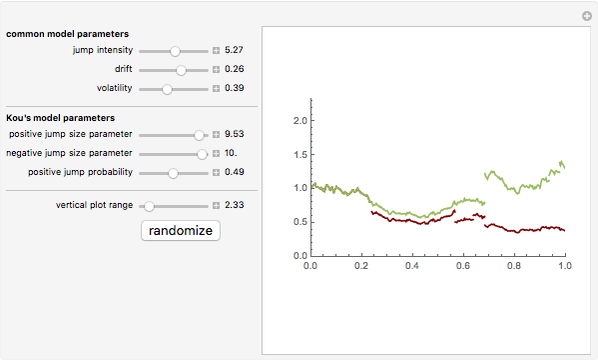
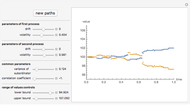
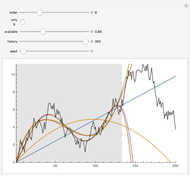
Jump diffusion processes are the simplest generalizations of the classical Black–Scholes model of stock price movements that include discontinuous jumps in price. This Demonstration compares the two most popular diffusion processes: the Merton model and the Kou model. One path from each model is shown. The models share the same continuous component and initial value but differ in their jump distributions, hence their trajectories coincide until the first jump of either process occurs. Kou's model, having 6 independent parameters versus Merton's model's five, is more flexible, hence we expressed the parameter's of Merton's models in terms of those of Kou's one. Thus the two paths shown have the same drift, diffusion as well as mean jump size and the standard deviation of jump sizes.
Contributed by: Andrzej Kozlowski (June 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The classical Black–Scholes model of stock price movements is known to suffer from a number of shortcomings. One of them is that the (log) returns distribution of empirical stock returns consistently show asymmetric leptocuritc features not present in the Black–Scholes model. In other words, the empirical return distribution is skewed to the left, and has a higher peak and two heavier tails than those of the normal distribution. Another feature is the so-called volatility smile. Yet another is the clear statistical evidence for the presence of discontinuous jumps in empirical prices, while the Black–Scholes model assumes that price trajectories are continuous.
One approach that successfully overcomes most of these difficulties while still retaining most of the tractability of the Black–Scholes model is to replace the exponential Brownian motion on which the Black–Scholes model is based by an exponential Lévy process. One group of such models are the so called "jump diffusion models". In these models the log stock price has two independent components: the "normal" evolution of prices is given by a diffusion process, punctuated by jumps at random intervals, that represent rare events, crashes, and large drawbacks. Two of the most popular models are Merton's jump diffusion model, in which the jumps in the log-price have a Gaussian distribution, and the Kou model in which they have asymmetric exponential distribution. More precisely, the distribution of jumps is  where
where  and
and  are exponential random variables with means
are exponential random variables with means  and
and  (
( and
and  are called the positive and negative jump size parameter in this Demonstration). The Kou model has a number of advantages over the better known Merton model. First of all, the model can produce more realistic heavier tails in the return distribution compared to the Merton model. Secondly, thanks to the memoryless property of the exponential distribution, explicit formulas can be obtained for many types of options. Thirdly, the presence of six parameters makes calibrating the model to fit empirical data easier.
are called the positive and negative jump size parameter in this Demonstration). The Kou model has a number of advantages over the better known Merton model. First of all, the model can produce more realistic heavier tails in the return distribution compared to the Merton model. Secondly, thanks to the memoryless property of the exponential distribution, explicit formulas can be obtained for many types of options. Thirdly, the presence of six parameters makes calibrating the model to fit empirical data easier.
S. G. Kou, "A Jump Diffusion Model for Option Pricing," Management Science, 48, 2002 pp.1086–1101.
S. G. Kou and H. Wang, "Option Pricing under a Double Exponential Jump Diffusion Model," Management Science, 50, pp. 1178–1192.
Permanent Citation
"Two Jump Diffusion Processes"
http://demonstrations.wolfram.com/TwoJumpDiffusionProcesses/
Wolfram Demonstrations Project
Published: June 16 2010