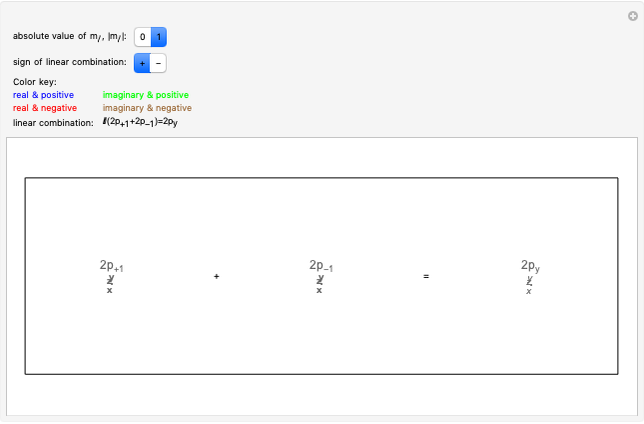
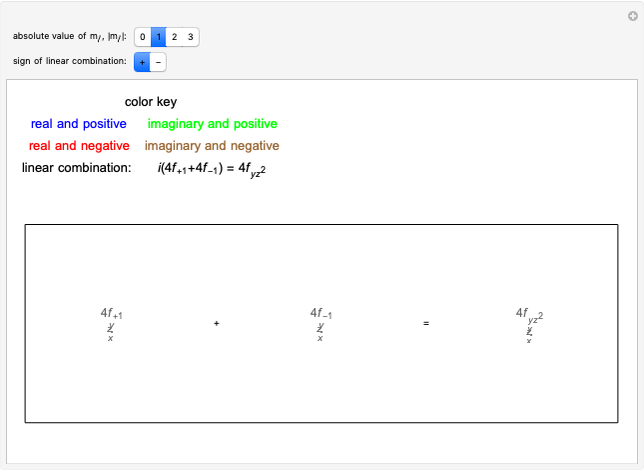
Rovibronic Spectrum of a Parallel Band of a Symmetric Rotor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
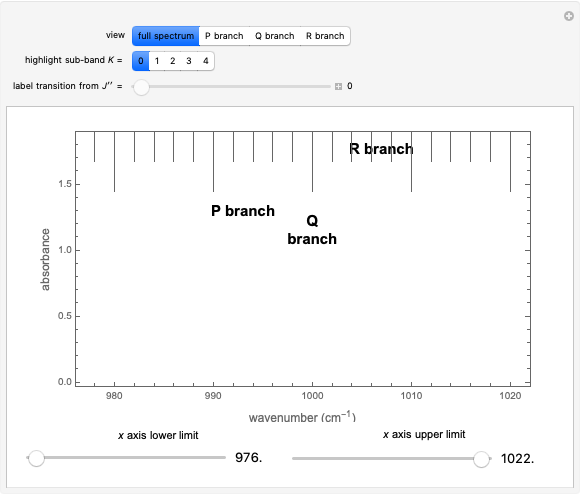
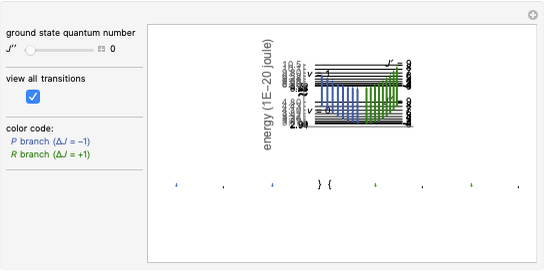
This Demonstration shows the rotationally resolved infrared spectrum of a parallel band of a symmetric rotor, with transitions occurring between nondegenerate vibrational levels. Symmetric rotors include ammonia  , benzene
, benzene 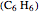 , and the methyl halides
, and the methyl halides 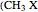 , where
, where 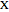 can be
can be 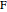 ,
, 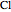 ,
, 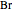 , or
, or 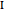 ). Symmetric rotors have two equal moments of inertia; the axis with the unique moment of inertia is termed the principle axis. For a symmetric rotor, the direction of the change in dipole moment, or transition moment, determines the appearance of the spectrum because different selection rules must be satisfied. If the transition moment is parallel to the principal axis, as in this Demonstration, a parallel band spectrum results. On the other hand, if the transition moment is perpendicular to the principal axis, a perpendicular band spectrum results. Hybrid bands can result if the transition moment has a component both parallel and perpendicular to the principal axis. For a parallel band, the vibrational selection rules are
). Symmetric rotors have two equal moments of inertia; the axis with the unique moment of inertia is termed the principle axis. For a symmetric rotor, the direction of the change in dipole moment, or transition moment, determines the appearance of the spectrum because different selection rules must be satisfied. If the transition moment is parallel to the principal axis, as in this Demonstration, a parallel band spectrum results. On the other hand, if the transition moment is perpendicular to the principal axis, a perpendicular band spectrum results. Hybrid bands can result if the transition moment has a component both parallel and perpendicular to the principal axis. For a parallel band, the vibrational selection rules are  and the rotational selection rules are
and the rotational selection rules are 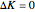 ,
, 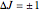 if
if 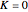 and
and 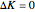 ,
, 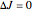 ,
, 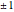 if
if 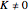 , with the restriction that
, with the restriction that 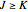 . If the complete band spectrum is deconstructed, it appears as a superposition of sub-bands. Each sub-band corresponds to a
. If the complete band spectrum is deconstructed, it appears as a superposition of sub-bands. Each sub-band corresponds to a 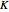 value and consists of a
value and consists of a 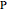 branch (
branch ( ,
, 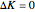 ,
, 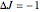 , smaller wavenumbers),
, smaller wavenumbers),  branch (
branch ( ,
, 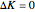 ,
, 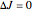 , middle branch, appears when
, middle branch, appears when 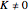 ), and
), and 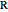 branch (
branch ( ,
, 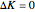 ,
, 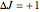 , larger wavenumbers). Due to the restriction that
, larger wavenumbers). Due to the restriction that 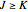 , with increasing
, with increasing 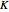 a decreasing number of lines are observed within each sub-band. The observed line intensities reflect a dependence on the thermal population of the ground state energy levels (determined by the Boltzmann factor) and the quantum numbers
a decreasing number of lines are observed within each sub-band. The observed line intensities reflect a dependence on the thermal population of the ground state energy levels (determined by the Boltzmann factor) and the quantum numbers 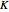 and
and 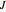 . With this Demonstration you can view the full spectrum and each branch individually. When viewing each branch individually, you can deconstruct the complete band by choosing which sub-band to highlight and by labeling individual lines/transitions within the sub-band. By using the
. With this Demonstration you can view the full spectrum and each branch individually. When viewing each branch individually, you can deconstruct the complete band by choosing which sub-band to highlight and by labeling individual lines/transitions within the sub-band. By using the  axis lower and upper limit controls, you can zoom in on any region of the spectrum.
axis lower and upper limit controls, you can zoom in on any region of the spectrum.
Contributed by: Whitney R. Hess and Lisa M. Goss (Idaho State University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this Demonstration, ground state constants and quantum numbers are denoted by a double prime (″) superscript and excited state constants and quantum numbers are denoted by a prime (′) superscript.
The mathematical expressions for simulating the spectrum assume that the centrifugal distortion constants 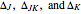 , and the anharmonicity constant,
, and the anharmonicity constant, 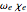 are negligible. The interaction of rotation and vibration is taken into account since the ground and excited state values for the rotational constants
are negligible. The interaction of rotation and vibration is taken into account since the ground and excited state values for the rotational constants 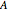 and
and 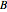 are not equal (
are not equal (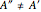 and
and 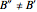 ). However, only a small difference between the ground and excited state values for these constants are used to simulate the spectrum, with
). However, only a small difference between the ground and excited state values for these constants are used to simulate the spectrum, with 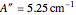 ,
, 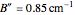 , and
, and 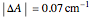 ,
, 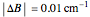 . The spectrum is simulated at a temperature of 30 Kelvin.
. The spectrum is simulated at a temperature of 30 Kelvin.
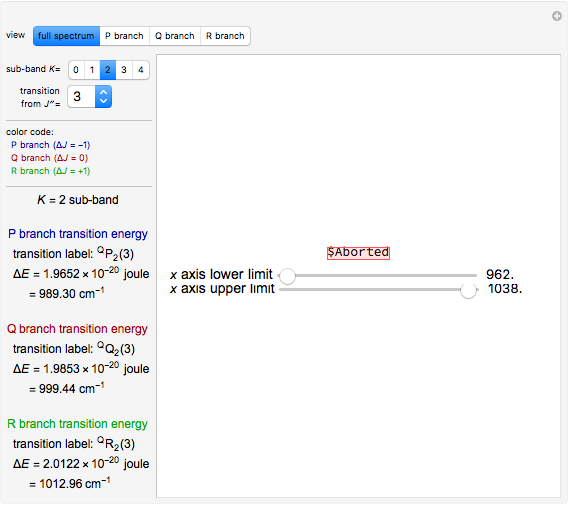
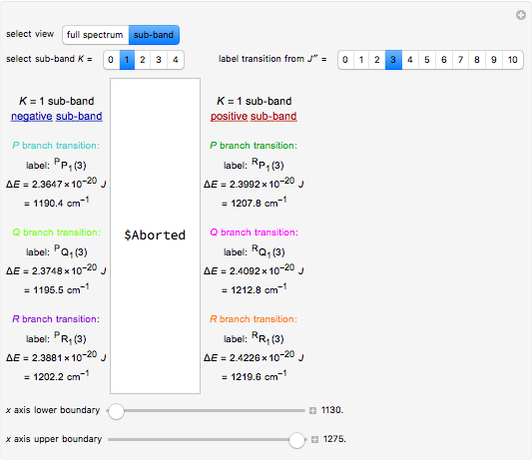
The spectral line corresponding to the chosen transition of interest is indicated by an arrow and labeled by 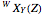 , with
, with 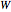 ,
, 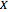 ,
, 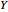 , and
, and 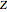 as follows.
as follows.
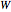 : transitions with
: transitions with 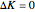 are designated with
are designated with 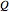 as a superscript, and all transitions in a parallel band fall into this category.
as a superscript, and all transitions in a parallel band fall into this category.
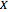 :
: 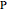 ,
,  , or
, or 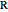 depends on which branch the line/transition resides.
depends on which branch the line/transition resides.
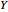 : the value of
: the value of 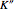 (ground state) is indicated by the subscript.
(ground state) is indicated by the subscript.
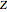 : the value of
: the value of 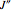 (ground state) is indicated in the parentheses.
(ground state) is indicated in the parentheses.
For example, 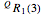 indicates the line corresponding to the
indicates the line corresponding to the 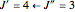 transition in the
transition in the 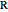 branch within the
branch within the 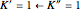 sub-band.
sub-band.
Snapshots 1, 2, 3, and 4: full spectrum, 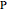 branch,
branch,  branch,
branch, 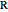 branch views, respectively. The text indicates which sub-band is highlighted and describes the energy levels associated with the chosen transition. The spectral line corresponding to the chosen transition is indicated by an arrow and labeled with the proper transition nomenclature described in this section.
branch views, respectively. The text indicates which sub-band is highlighted and describes the energy levels associated with the chosen transition. The spectral line corresponding to the chosen transition is indicated by an arrow and labeled with the proper transition nomenclature described in this section.
Snapshot 5: with increasing 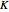 , a decreasing number of lines are observed in the beginning of each branch of a sub-band. For example, in the
, a decreasing number of lines are observed in the beginning of each branch of a sub-band. For example, in the 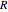 branch within the
branch within the 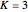 sub-band, there are no transitions from
sub-band, there are no transitions from 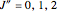 due to the restriction that
due to the restriction that 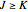 .
.
References
[1] P. Atkins and J. de Paula, Physical Chemistry, New York: Oxford University Press, 2006.
[2] G. Herzberg, Molecular Spectra and Molecular Structure II. Infrared and Raman Spectra of Polyatomic Molecules, Princeton, NJ: D. Van Nostrand Company, Inc., 1945.
Permanent Citation