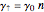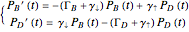Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Rate Equations for a Three-Level Model in Low-Dimensional Exciton Systems

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

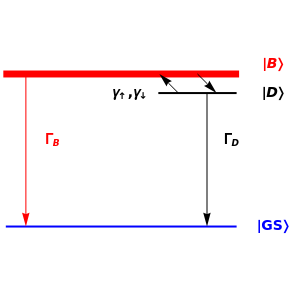
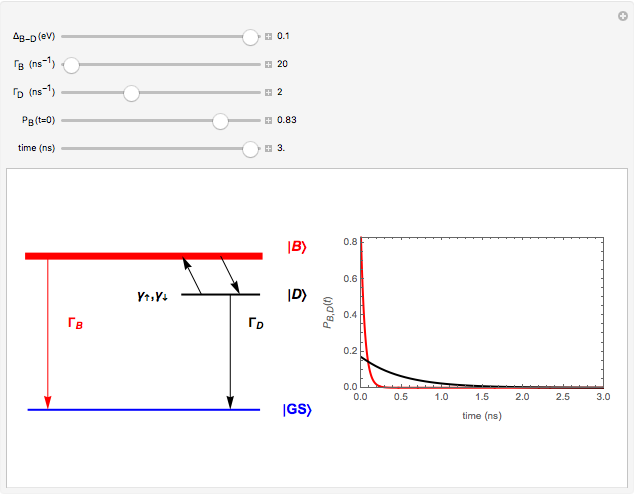
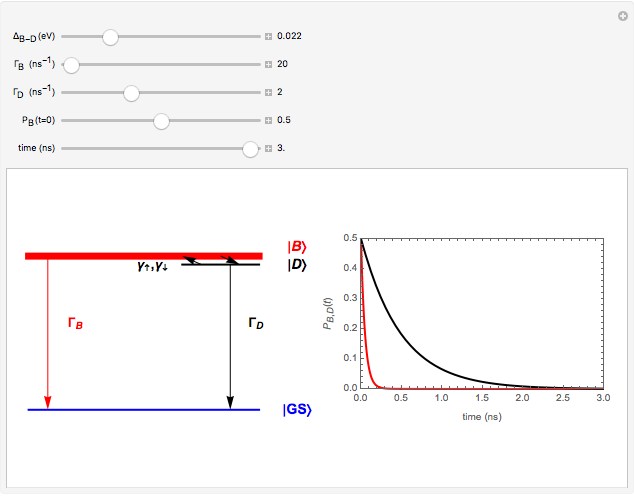
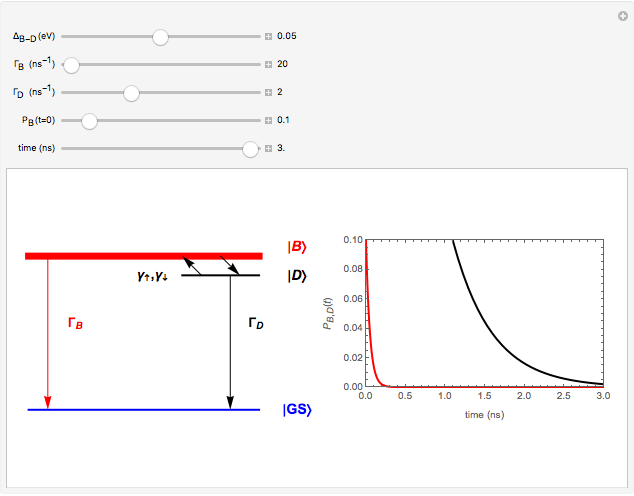
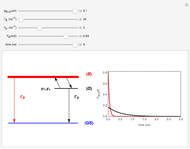
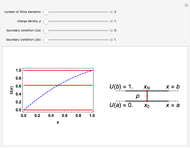
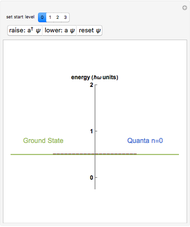
This Demonstrations shows a three-level scheme useful for describing the luminescence decays of low-dimensional quantum systems, such as single-walled carbon nanotubes and quantum dots. The excited-state photophysics of these systems can be modeled with an optically active exciton state, namely bright exciton , with an optically forbidden level below, known as dark exciton , separated by a splitting energy 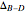(of the order of a few meV). Recombination from both levels to the electronic ground state 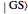is recovered by the related rates (mainly nonradiative) and (purely nonradiative), respectively. The inverse quantities give the lifetimes of these excitons.

[more]

Thermalization between dark and bright states can occur through coupling to acoustic phonon modes, involving one phonon absorption and emission process, with upward and downward scattering rates, where is the phonon occupation number given by the Bose–Einstein distribution function and is the temperature-independent scattering rate (set to a typical value of 0.05 for simplicity).

The kinetic equations for the bright and dark state populations and as a function of time are given by the following system of coupled differential equations:

This Demonstration implements the numerical solution of this system of equations and lets you explore dynamically the solutions at a given temperature as a function of scattering rates, bright-dark energy splitting, and the initial population of bright state . The initial population of the dark state is set to .

[less]

Contributed by: Jessica Alfonsi (March 2011)
(University of Padova, Italy)
Open content licensed under CC BY-NC-SA

Snapshots

Details

For more information, see [1], [2], and [3]. In [3] is a treatment of spin-flip processes using the Fermi-Dirac distribution function, but with similar rate equations as in [1] and [2].

References

[1] T. Gokus, L. Cognet, J. G. Duque, M. Pasquali, A. Hartschuh, and B. Lounis, "Mono- and Biexponential Luminescence Decays of Individual Single-Walled Carbon Nanotubes," Journal of Physical Chemistry C 114(33), 2010 pp. 14025–14028.

[2] R. Matsunaga, Y. Miyauchi, K. Matsuda, and Y. Kanemitsu, "Symmetry-Induced Nonequilibrium Distributions of Bright and Dark Exciton States in Single Carbon Nanotubes," Physical Review B, 80, 2009 p. 115436.

[3] P. A. Dalgarno, J. M. Smith, B. D. Gerardot, A. O. Govorov, K. Karrai, P. M. Petroff, and R. J. Warburton, "Dark Exciton Decay Dynamics of a Semiconductor Quantum Dot," Physica Status Solidi A 202(14), 2005 pp. 2591–2597.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send