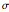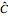Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

How Do Confidence Intervals Work?

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

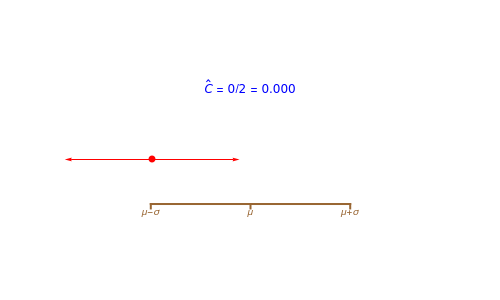
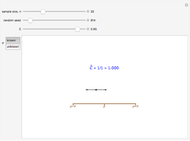
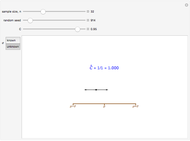
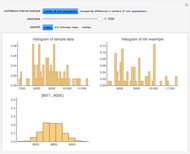
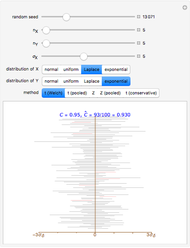
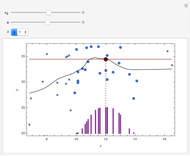
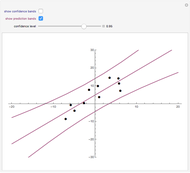
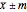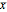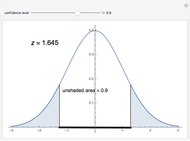
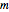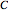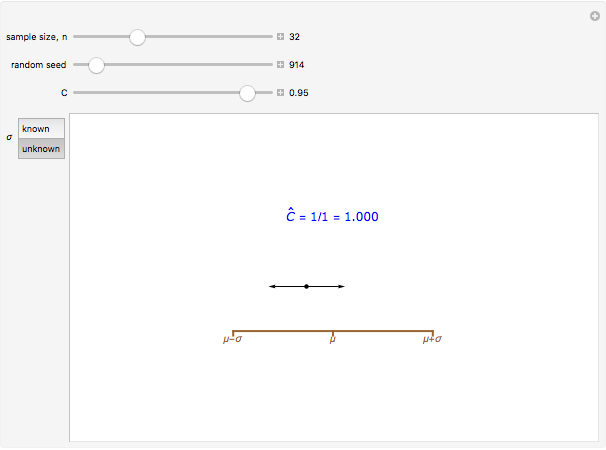
This Demonstration shows the confidence interval, , for based on random samples of size from a normal population with mean and standard deviation , where is the sample mean and is the margin of error for a level interval. There are two cases, corresponding to when is assumed known, or is not known and is estimated by the standard deviation in the sample. For the known case, 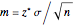, where the critical value 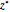is determined so that the area to the right of 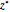is 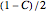. Similarly in the unknown case, , where is the sample standard deviation and 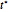is the critical value determined from a -distribution with degrees of freedom.

[more]

Five things to see in this Demonstration:

1. The width of the confidence interval increases as increases.

2. The width of the confidence interval decreases as increases.

3. For fixed and , the width of the confidence interval in the known case is fixed, but it is stochastic when is unknown due to the variation in the sample standard deviation, . The stochastic property can be seen by varying the random seed when unknown is selected.

4. The width of the confidence interval tends to be larger in the unknown case but the difference decreases as increases.

5. Running an animation varying the random seed, we can obtain an empirical estimate of the coverage probability. Try slowing the animation down to get a large number of repetitions. The intervals are color coded: black when the interval covers and red when it misses. The animation demonstrates the stochastic coverage probability of the interval.

[less]

Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

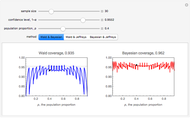
If we assume that , the unknown mean, has a suitable noninformative prior, the confidence interval with level 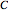confidence is equivalent to the highest posterior density interval [1] p. 85 and p. 98, and we can make the natural statement that .

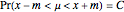[1] G. E. P. Box and G. C. Tiao, Bayesian Inference in Statistical Analysis, Reading: Addison-Wesley, 1973.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send