Simulation of 1D Diffusion Using the Monte Carlo Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
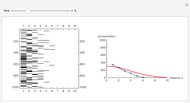
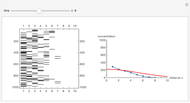
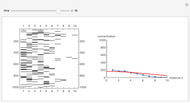
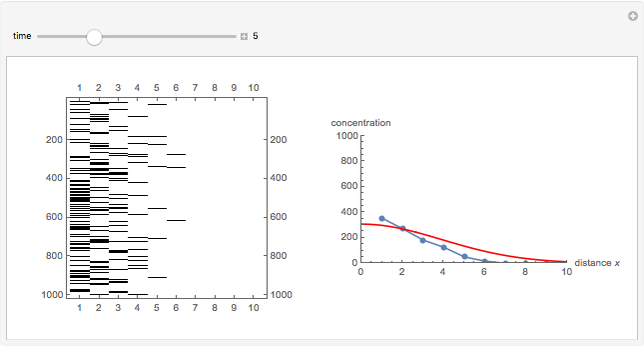
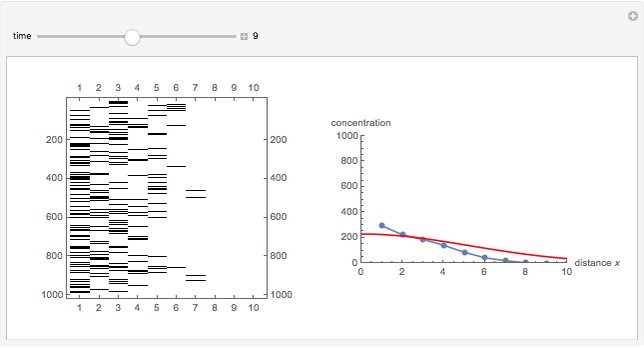
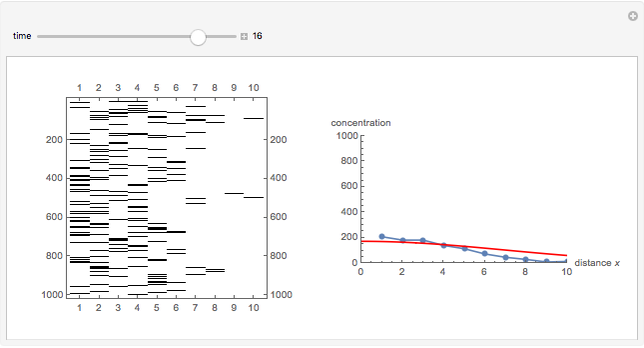
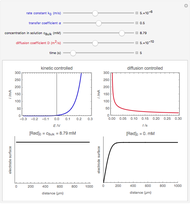
This Demonstration simulates the diffusion process in one dimension, which obeys the equation  , using a Monte Carlo method.
, using a Monte Carlo method.
Contributed by: Quang-Dao Trinh (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
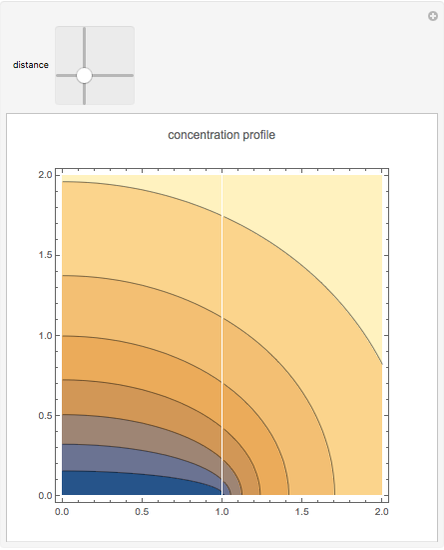
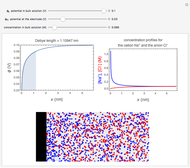
At time  , there are 1000 points at the left edge of the box, representing the initial condition at
, there are 1000 points at the left edge of the box, representing the initial condition at  . At each time step, these 1000 points will diffuse by a random walk (Monte Carlo simulation) along the box. The concentration
. At each time step, these 1000 points will diffuse by a random walk (Monte Carlo simulation) along the box. The concentration  at distance
at distance  is the density (number of points) at that position.
is the density (number of points) at that position.
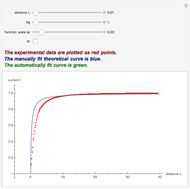
The analytical solution of the equation is 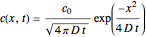 , where
, where 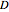 is the diffusion coefficient and
is the diffusion coefficient and  is the initial concentration, shown as the red curve. The concentration profiles using Monte Carlo simulation are shown as blue dots.
is the initial concentration, shown as the red curve. The concentration profiles using Monte Carlo simulation are shown as blue dots.
Permanent Citation