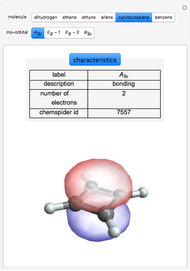
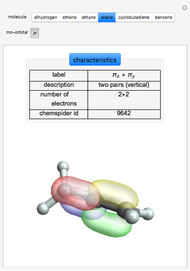
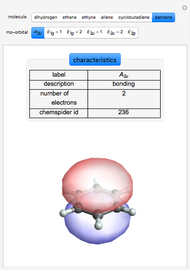
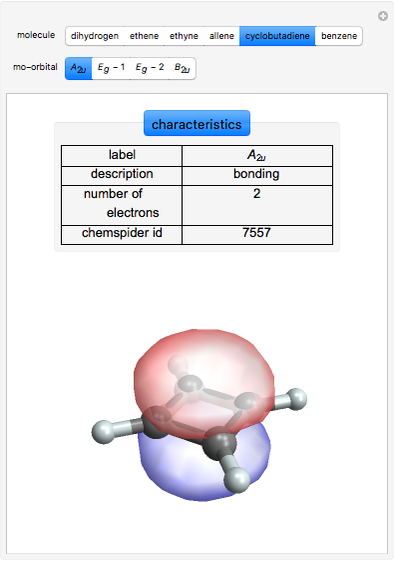
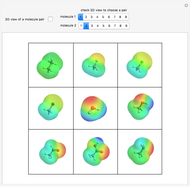
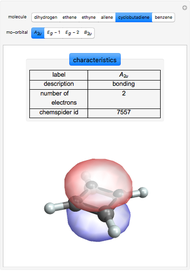
Some Examples of Molecule Orbitals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Molecule orbitals are formed when atomic orbitals overlap. Mathematically, this is represented by a linear combination of atomic orbitals (as in the LCAO-MO method). Some possible classifications of orbitals are bonding and antibonding and  - and
- and  -symmetry.
-symmetry.
Contributed by: Guenther Gsaller (October 2013)
Suggested by: Norbert Mueller
(Institute of Organic Chemistry, Johannes Kepler University, Linz, Austria, www.jku.at/orc)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The atomic orbitals used in this Demonstration are the following Slater-type orbitals:
 ,
,
 ,
,
 ,
,
 .
.
For ethene, the LCAO-MO method gives two normalized  molecule orbitals:
molecule orbitals:
 ,
,
 .
.
The formula for the distance of two points in three-dimensional space can be used to rewrite the wavefunctions with the corresponding  -Slater orbital (
-Slater orbital ( … interatomic distance):
… interatomic distance):
 ,
,
 .
.
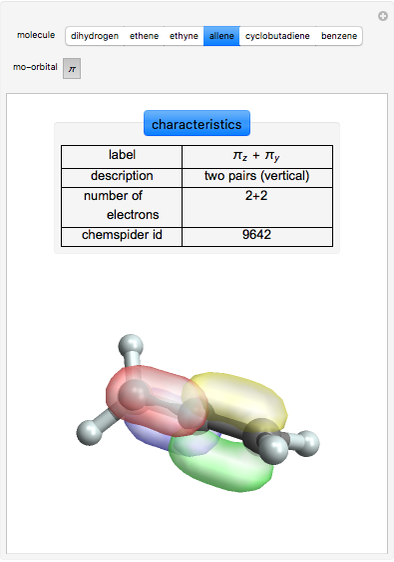
The diagrams for the molecular orbitals for dihydrogen, ethyne, and allene can also be written using the separation-dependent formula.
The simple Hückel method (SMO) is a rudimentary method for energies and orbitals of  -electron systems. An essential step is solving the secular equations.
-electron systems. An essential step is solving the secular equations.
For cyclobutadiene, the secular equations are:
 ,
,
which can be reduced to
 .
.
Taking symmetry into account, one can factorize this secular determinant into two separate determinants:


yielding the solutions  , and
, and  .
.
The four corresponding LCAO molecular orbitals are found using cofactors:
 ,
,
 ,
,
 ,
,
 .
.
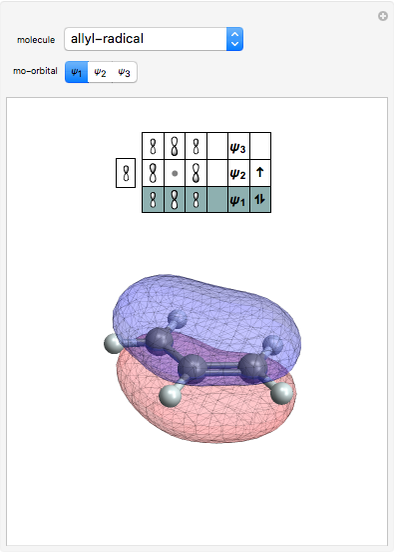
An alternative set for cyclobutadiene is:
 ,
,
 ,
,
 ,
,
 .
.
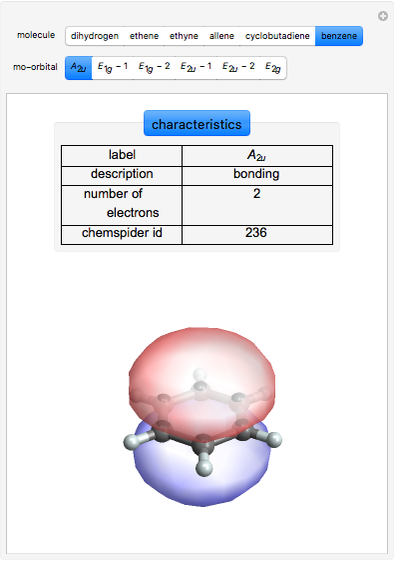
Similarly for benzene, from the secular determinant,

can be factorized to give the wavefunctions:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Cyclic  -sytems (such as cyclobutadiene and benzene) can be rewritten with the corresponding
-sytems (such as cyclobutadiene and benzene) can be rewritten with the corresponding  -Slater orbitals in the complex exponential form:
-Slater orbitals in the complex exponential form:
 ,
,
with  .
.
ChemSpider [1] is the source for the ball and stick figures. The ChemSpider IDs for each structure used are listed in the code for the Demonstration.
References
[1] Royal Society of Chemistry. ChemSpider. (Oct 8, 2013) www.chemspider.com.
[2] H. E. Zimmerman, Quantum Mechanics for Organic Chemists, London: Academic Press, 1975.
[3] A. Rauk, Orbital Interaction Theory of Organic Chemistry (2nd ed.), New York: John Wiley & Sons, 2000.
Permanent Citation