Some Irreptiles of Order Greater than 20

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
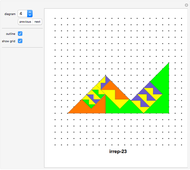
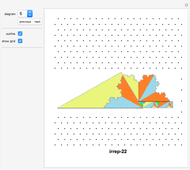
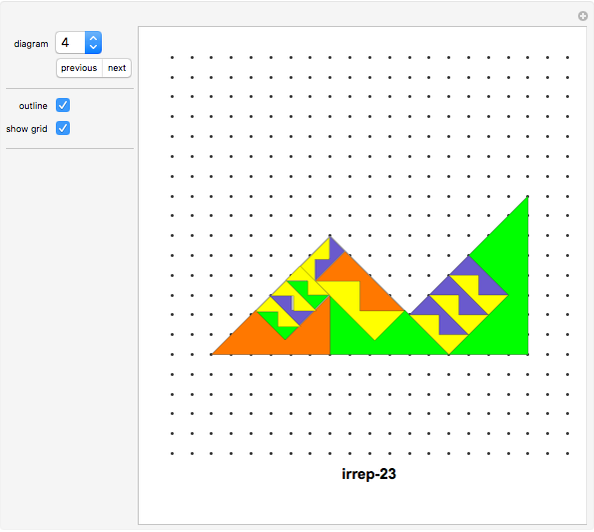
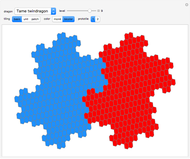
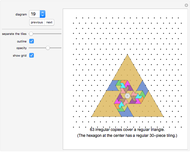
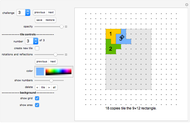
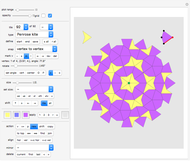
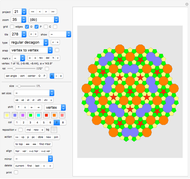
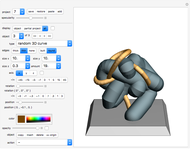
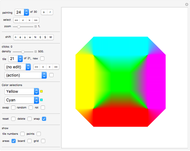
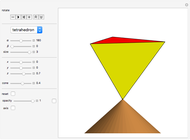
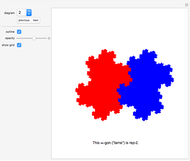
A rep-tile is a shape that can be tiled with smaller equally sized copies of the shape. If the tiling uses  copies, the shape is said to be rep-
copies, the shape is said to be rep- .
.
Contributed by: Karl Scherer (May 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
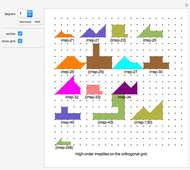
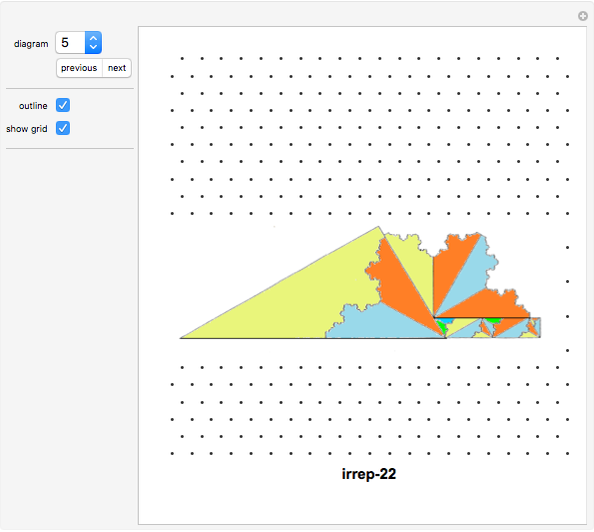
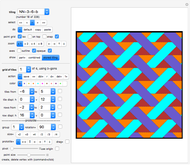
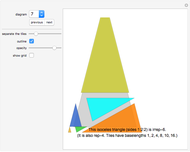
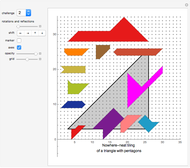
The order of an irreptile is the smallest number greater than 1 of tiles needed for the tiling. This Demonstration shows a collection of irreptiles of order greater than 20.
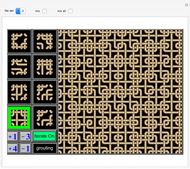
Diagrams 6, 10, 25, 33 do not show a tiling because I could not find the associated tiling. I hope a reader can fill in some of the gaps.
Order
Irreptiles of order less than 20 were dealt with in the Demonstration Irreptilesby the same author.
The regular order of a shape is the smallest possible number of tiles in a regular self-tiling.
The irregular order of a shape is the smallest possible number of tiles in an irregular self-tiling (using more than one size of tile).
The author conjectures that there is no shape when these orders are the same.
History
The terms "irreptile" and "puritile" were introduced by the author in 1987 in his book A Puzzling Journey to the Reptiles and Related Animals, privately published. Since then several mathematicians have expanded on the subject in various ways.
The material of this Demonstration was mainly taken from the author's book.
Of course, this Demonstration can only give a short introduction to irreptiles. Many questions can be asked (and many are answered in the author's book), but several problem areas are still unsolved.
Content of this Demonstration
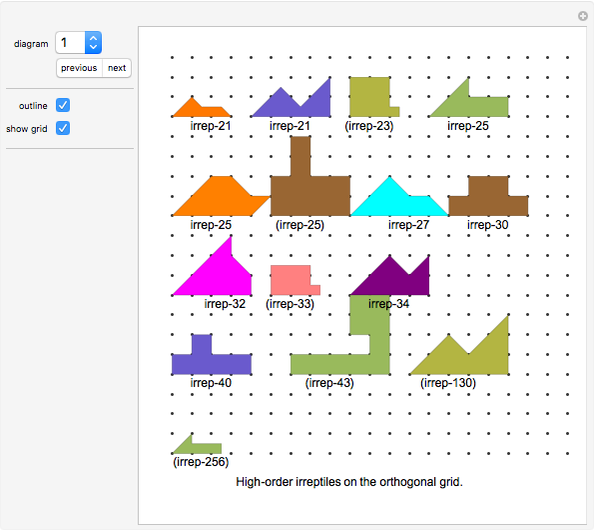
Diagrams 1 and 2 are overviews. The icons with names in parentheses have the self-tiling missing.
If you know the solution to a missing tiling, please contact the author (karlscherer.com).
If a shape is a polysquare such that two copies tile a rectangle, then the associated regular and irregular self-tilings are usually quite straightforward and obvious, if not trivial. Therefore some of these cases have been ignored in this Demonstration.
Permanent Citation