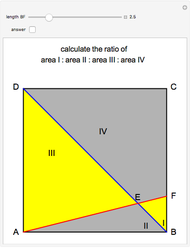
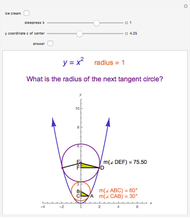
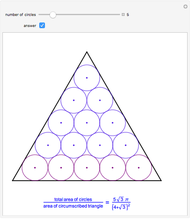
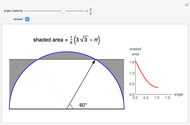
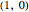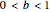Swing the Logarithmic Curve around (1, 0)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
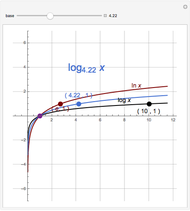
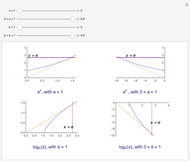
The logarithmic function to the base  , where
, where  and
and  , is defined by
, is defined by 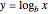 if and only if
if and only if  ; the domain is
; the domain is  and the range is
and the range is  .
.
Contributed by: Abraham Gadalla (March 2011)
Open content licensed under CC BY-NC-SA
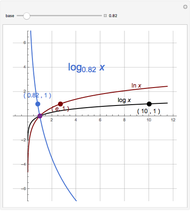
Snapshots
Details
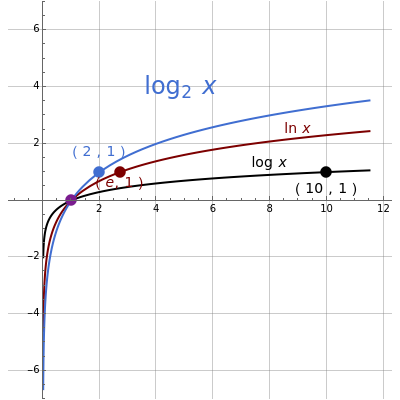
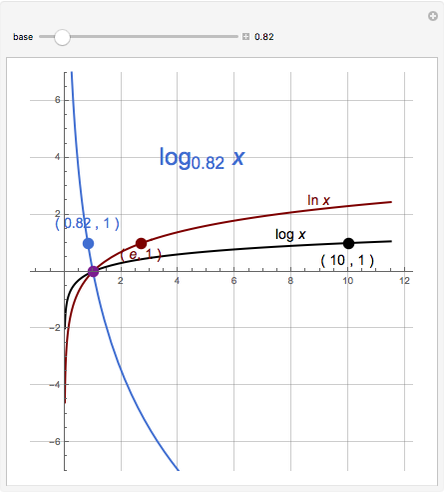
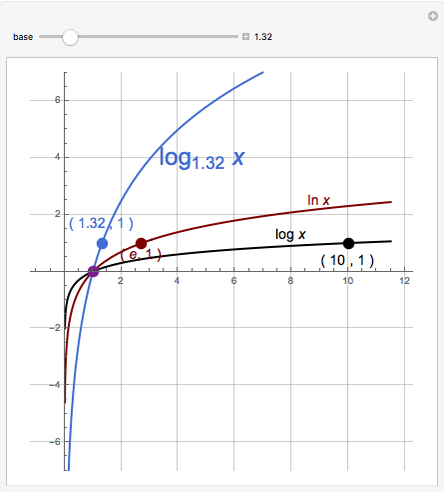
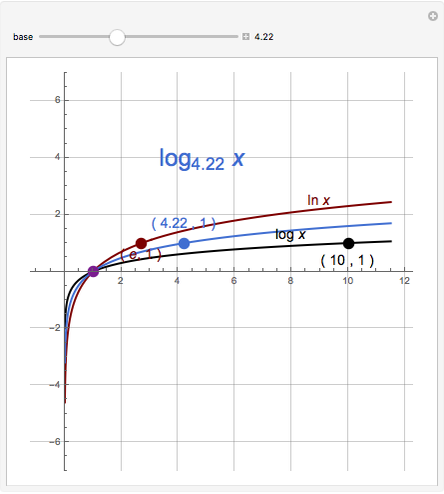
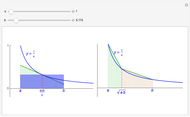
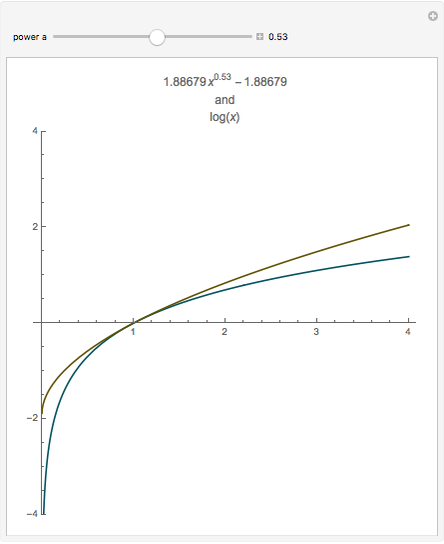
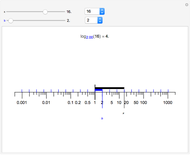
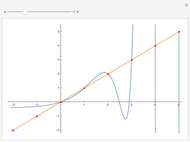
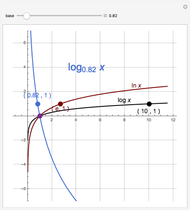
When considering the common logarithm (i.e., base 10), we notice that as the  values decrease from 1 to 0, the curve falls rapidly, and for
values decrease from 1 to 0, the curve falls rapidly, and for  , it approaches the negative
, it approaches the negative 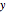 axis asymptotically. As the
axis asymptotically. As the  values increase from 1 to 10, the function increases monotonically from 0 to 1, and as
values increase from 1 to 10, the function increases monotonically from 0 to 1, and as  values increase by a factor of 10 (for example, from 10 to 100) the function increases from 1 to 2. The same applies for the intervals
values increase by a factor of 10 (for example, from 10 to 100) the function increases from 1 to 2. The same applies for the intervals 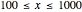 ,
,  , and so on. Because the changes are very small for such large intervals, the curve can be well approximated by a straight line.
, and so on. Because the changes are very small for such large intervals, the curve can be well approximated by a straight line.
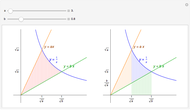
To switch bases, we let  ; we will show that
; we will show that  .
.
By definition,  implies
implies 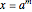 .
.
Taking the 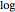 to the base
to the base  of both sides gives
of both sides gives  .
.
Dividing by  gives
gives 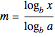 . Replacing
. Replacing  by
by  yields
yields  .
.
Permanent Citation