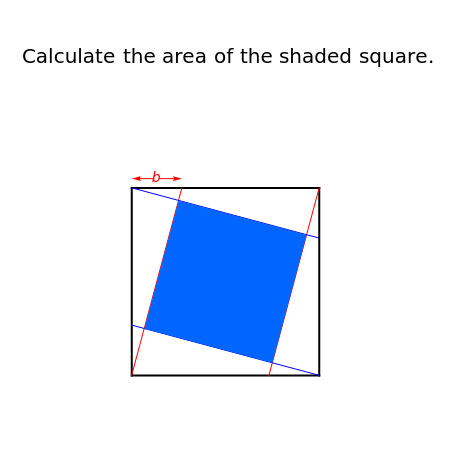
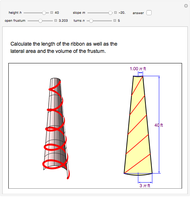
The Area of a Square in a Square

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
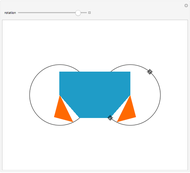
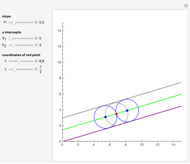
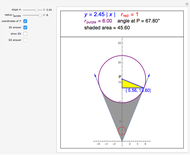
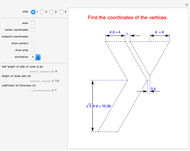
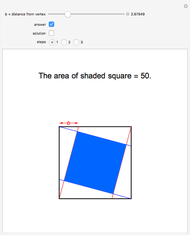
Given a square with side length  and parallel lines with slopes
and parallel lines with slopes 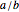 and perpendicular lines with slopes
and perpendicular lines with slopes 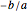 , find the area of the shaded square. Also find the ratio
, find the area of the shaded square. Also find the ratio 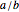 that makes the area of the inner square equal to 50% of the outer square.
that makes the area of the inner square equal to 50% of the outer square.
Contributed by: Abraham Gadalla (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
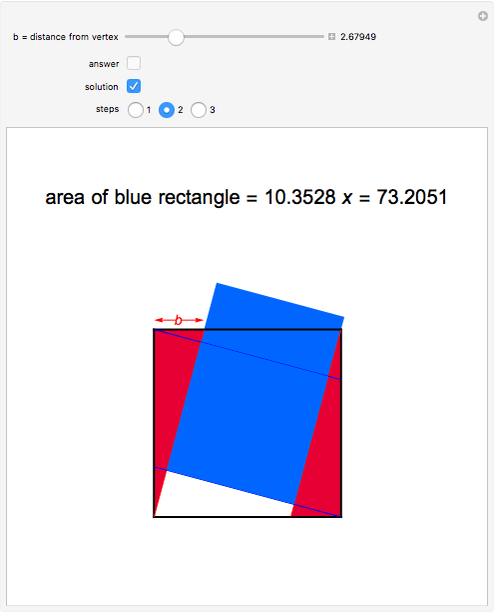
The problem can be solved in many ways. The solution illustrated here is visual. It is done in three steps:
Step 1:
The area of the parallelogram = area of square – area of two red triangles =  .
.
Step 2:
Cut the trapezoidal piece from the bottom of the parallelogram and attach it to the top. The parallelogram becomes a rectangle with its base on the base of the inner square. The length of the parallelogram is (according to the Pythagorean theorem) 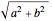 . That is the length of the shaded rectangle, and its width is to the length of the side of the inner square,
. That is the length of the shaded rectangle, and its width is to the length of the side of the inner square,  .
.
The area of the shaded rectangle = base × height =  = the area of the parallelogram.
= the area of the parallelogram.
Therefore: 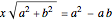 , and so
, and so 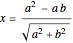 .
.
Step 3:
The required area of the inner square is 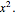
Permanent Citation