Tax Deferral

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
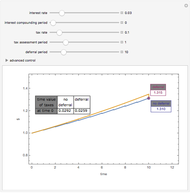
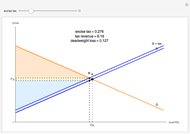
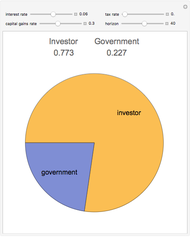
Investment income can be taxed in several ways by the government. In the United States, tax law generally chooses for each class of investment whether to tax growth in the value of the investment on an annual basis (even if the investor does not withdraw any funds) or defer taxation until a gain is "realized" by the investor, usually through withdrawing funds from the investment. This latter tax is often referred to as a "capital gains tax" and is generally applied to the difference between the value of the investment at the time of "realization" and the "basis" in the investment, generally the amount of money actually put into the investment over time.
[more]
Contributed by: Seth J. Chandler (September 2019)
Open content licensed under CC BY-NC-SA
Details
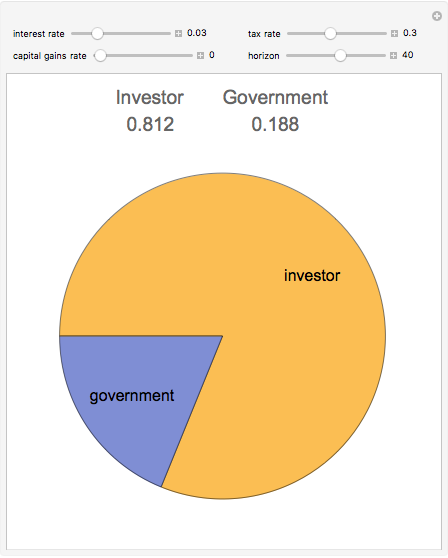
The formula for the share of the investor is:
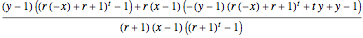 ,
,
where  is the tax rate on annual investment growth,
is the tax rate on annual investment growth,  is the tax rate on capital gains,
is the tax rate on capital gains,  is the interest rate and
is the interest rate and  is the time horizon. The government's share is one minus the investor's share.
is the time horizon. The government's share is one minus the investor's share.
This formula is derived as follows:
Step 1: Let  be the amount invested by the taxpayer each year. Assume the tax is paid at the end of the year. Solve the dual recurrence equations
be the amount invested by the taxpayer each year. Assume the tax is paid at the end of the year. Solve the dual recurrence equations 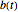 and
and  , where
, where 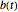 represents the taxpayer's account and
represents the taxpayer's account and 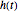 represents the government's account after payment of income taxes but before consideration of any capital gains tax. Both accounts are set to zero at time 0.
represents the government's account after payment of income taxes but before consideration of any capital gains tax. Both accounts are set to zero at time 0. 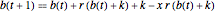 \:201a and
\:201a and 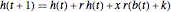 . The solutions to these equations, which can be found using the Wolfram Language RSolveValue function, are
. The solutions to these equations, which can be found using the Wolfram Language RSolveValue function, are 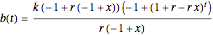 and
and 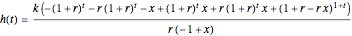 .
.
Step 2: Now recognize that the capital gains payable at time  is the capital gains tax rate
is the capital gains tax rate 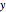 multiplied by the difference between
multiplied by the difference between 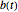 and
and 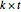 , the latter of which is the amount of money paid in by the taxpayer (the so-called "basis").
, the latter of which is the amount of money paid in by the taxpayer (the so-called "basis").
Step 3: Subtract the capital gains tax from the taxpayer's account and call it 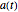 ; add the capital gains tax to the government's account and call it
; add the capital gains tax to the government's account and call it 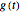 . Some algebra shows the results are
. Some algebra shows the results are 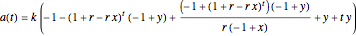 and
and 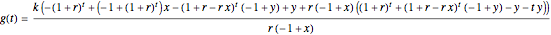 .
.
Step 4. Now divide the taxpayer's post-capital gains account 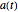 by the total
by the total 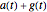 to get the taxpayer's share; divide the government's post-capital gains account
to get the taxpayer's share; divide the government's post-capital gains account 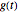 by the total
by the total 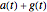 to get the government's share. The
to get the government's share. The  's in both equations cancel out and the results are
's in both equations cancel out and the results are 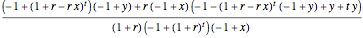 and
and 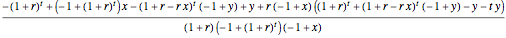 , respectively. One can check that the results are plausible by adding the two values together; the result is 1.
, respectively. One can check that the results are plausible by adding the two values together; the result is 1.
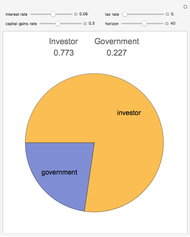
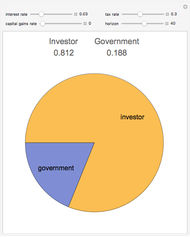
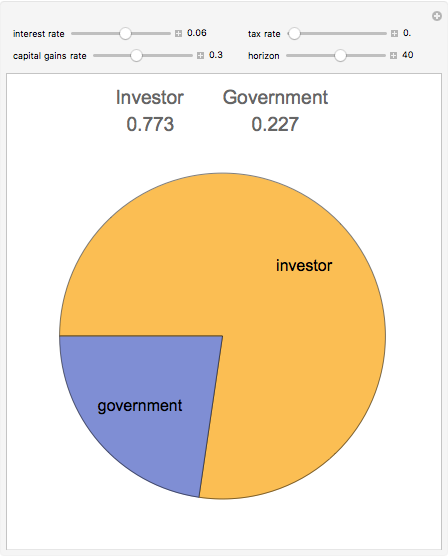
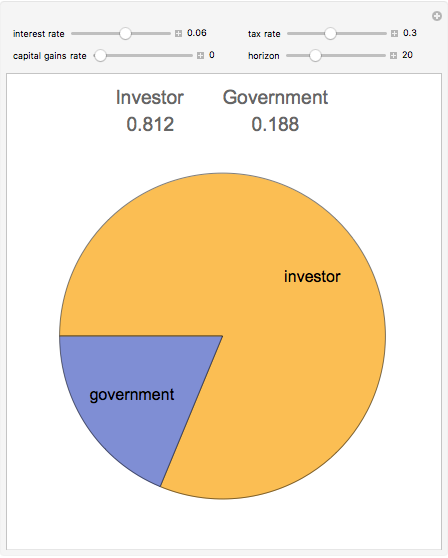
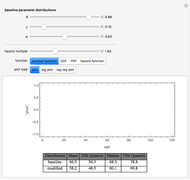
Snapshot 1: reducing the time horizon reduces the government's share
Snapshot 2: lowering the interest rate reduces the government's share
Snapshot 3: treating the investment growth as "ordinary income" results in a greater government share than deferral resulting from treatment as a "capital gain"
Reference
[1] A. Auerbach, "Retrospective Capital Gains Taxation," National Bureau of Economic Research, Working Paper No. 2792, 1988. (Aug 22, 2019) www.nber.org/papers/w2792.pdf.
Snapshots
Permanent Citation