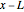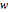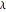Liability Insurance Desirability under Lognormal Loss Distributions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider an entity facing potential liability that has purchased a liability insurance contract providing that it will pay a third party up to an amount  if a judgment is rendered. If the insured could act selfishly, it would prefer an insurance contract that would "diminish": it would specify that in the event a judgment against the insured would, even with the existence of the liability insurance, bankrupt the insured, the insurer should pay nothing. This is so because payments to a third party in such a setting do essentially nothing to help the insured, but drive up the cost of premiums because the insurer must pay. Either as the result of regulation or custom, however, such "diminution" provisions are generally unlawful. This is so because diminution might otherwise prevent victims from being compensated more fully when individuals with liability insurance injure them. This restriction on freedom of contract means, however, that there are some settings in which insureds, even though they might like to transfer risk, find it undesirable to do so.
if a judgment is rendered. If the insured could act selfishly, it would prefer an insurance contract that would "diminish": it would specify that in the event a judgment against the insured would, even with the existence of the liability insurance, bankrupt the insured, the insurer should pay nothing. This is so because payments to a third party in such a setting do essentially nothing to help the insured, but drive up the cost of premiums because the insurer must pay. Either as the result of regulation or custom, however, such "diminution" provisions are generally unlawful. This is so because diminution might otherwise prevent victims from being compensated more fully when individuals with liability insurance injure them. This restriction on freedom of contract means, however, that there are some settings in which insureds, even though they might like to transfer risk, find it undesirable to do so.
Contributed by: Seth J. Chandler (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
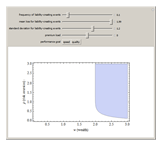
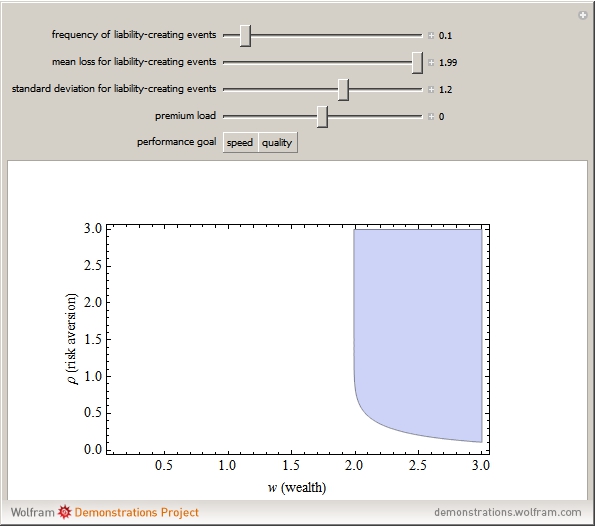
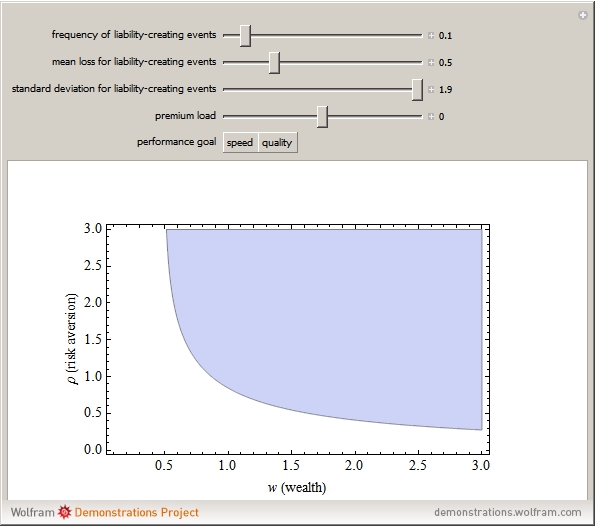
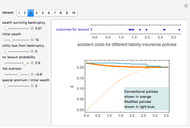
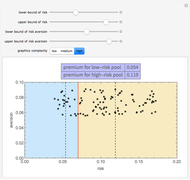
The combinations of wealth and risk aversion that result in full insurance shrink when:
Snapshot 1: mean losses are larger
Snapshot 2: the standard deviation of losses is larger
Snapshot 3: the premium load is greater
This Demonstration makes use of the Mathematica compiler to achieve additional speed. It also has used Experimental'OptimizeExpression in order to develop efficient primitives in the computation of premium and residual risk.
The method of parameterizing risk aversion used in this Demonstration is somewhat unorthodox, but has the virtue of achieving a closed-form solution. The idea is basically to treat risk aversion as if you were drawing from a distribution shaped similarly to the original distribution but with a higher mean. Here, in computing risk, we draw from a distribution with mean 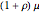 , which collapses to
, which collapses to  if risk aversion
if risk aversion  is zero. The idea derives from the concept of spectral measures which, as discussed by the author here, is similar to drawing from an
is zero. The idea derives from the concept of spectral measures which, as discussed by the author here, is similar to drawing from an 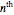 -order distribution of
-order distribution of  observations of a loss distribution. Such an order distribution generally results in higher draws than the original distribution. Thus, drawing from an order distribution is similar to drawing from a distribution that is shaped similarly but has a higher mean. It is thus a reasonable way of simulating risk aversion.
observations of a loss distribution. Such an order distribution generally results in higher draws than the original distribution. Thus, drawing from an order distribution is similar to drawing from a distribution that is shaped similarly but has a higher mean. It is thus a reasonable way of simulating risk aversion.
A lognormal distribution is used here because (a) judgments in lawsuits are sometimes modeled as emerging from lognormal distributions; and (b) it results in a closed-form solution to the problem at hand when used in conjunction with the method described above for risk aversion. The principles shown in this Demonstration are likely to be applicable, however, to a broader class of loss distributions. The key is to be able to scale the wealth of the insured available for execution to some metric of the distribution, such as the upper bound of its domain, or some high quantile of the distribution.
The lognormal distribution employed in the code here has been reparameterized to permit more direct representation of mean and standard deviation.
Although most liability insurance contracts contain a clause prohibiting the insurer from reducing the amount it pays a third party based on their insured's insolvency, some insurance contracts do not. Notably, reinsurance contracts sometimes do not have such a clause nor do some maritime insurance policies.
The expression for the premium is derived from evaluating the following Mathematica expression:
Simplify[(1 + λ) f Mean[CensoredDistribution[{0, L}, LogNormalDistribution2[μ, σ]]]]
The expression for the value of the residual risk is derived from evaluating the following Mathematica expression:
Simplify[f Mean[CensoredDistribution[{0, w}, TransformedDistribution[x - L, Distributed[x, LogNormalDistribution2[μ (1 + ρ), σ]] ]]]]
References
[1] S. Shavell, "The Judgment Proof Problem," International Review of Law and Economics 6, 1986 pp. 45–58.
[2] S. Chandler, "A 'Genetically Modified' Liability Insurance Contract," University of Connecticut Insurance Law Journal, 13(2), 2007 pp. 203–265. insurancejournal.org/wp-content/uploads/2011/07/15.pdf.
Permanent Citation