Tetrads

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
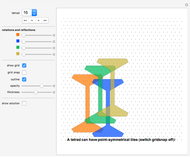
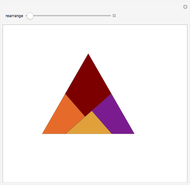
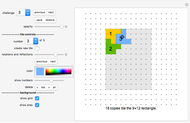
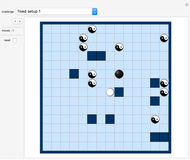
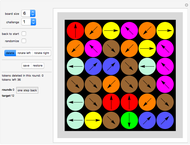
Rearrange the four given tiles so that each tile shares some boundary (of positive measure) with the other three tiles. Such an arrangement is called a "tetrad".
[more]
Contributed by: Karl Scherer (April 2008)
Additional contributions: Frank Rubin, Scott Kim, Juris Čerņenoks, Robert Ammann, Greg Frederickson, Jean L. Loyer, Livio Zucca
Open content licensed under CC BY-NC-SA
Snapshots
Details
Definition
A tetrad is a union of four (simply connected) congruent shapes that are placed without overlapping in such a way that each shape shares some boundary (of positive measure) with each of the other three shapes.
Most Important Findings
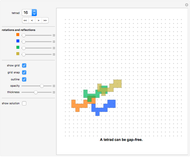
No tetrad can be made out of four congruent convex regions. Several examples exist (for both the symmetric and asymmetric case) of curved tiles with only one vertex, four copies of which form a simply connected tetrad. This is the lowest number of vertices per tile known for this problem. One is also the absolute minimum of vertices per tile, because whenever three shapes meet at one point, at least one of the three boundary lines must have a vertex (cusp) at this point. Hence a simply connected tetrad cannot be constructed from four tiles (congruent or not) that have smoothly rounded boundaries. One can tile the plane with a simply connected tetrad formed from congruent tiles; see examples.
Types of Tetrads
Tetrads where the four shapes join without gaps (i.e., simply connected tetrads). Tetrads consisting of four congruent shapes. Such a tetrad is called a congruent tetrad for short. Simply connected tetrads consisting of four congruent shapes. This is a combination of the two conditions above. Some polysquare reptiles can form such simply connected congruent tetrads. There are also some polyiamond and polytan solutions to this mathematical puzzle. It is still an unsolved problem whether a simply connected congruent tetrad can be convex. Tetrads consisting of four similar shapes (i.e., figures of same shape, but with different sizes). Such a tetrad is called a similar tetrad for short. In contrast to congruent tetrads, a simply connected similar tetrad can be convex; even better: it can have the shape of a square.
Areas of Interest
From the previous paragraphs you see that the following properties of tetrads are worth investigating: Does the tetrad have gaps or is it simply connected? Are its four parts congruent/similar/neither? Are its four parts symmetric/asymmetric? Are its four parts polysquares/polyiamonds/polytans/polyhexes/other? Can the four parts have curved outlines/partly curved outlines/fractal outlines? If the four parts are partially curved, how many vertices do the parts need at least? Can you find a solution for any given number of vertices? This game shows examples of convex simply connected tetrads with pieces which have any number of vertices apart from 2, 3, or 5. Can one find solutions for these three missing cases? Is the outline of the tetrad convex or not? Can the outline be a square? Is the tetrad symmetric or asymmetric? How many vertices does the outline of a tetrad have at least? Do the tiles have to have straight lines as part of their outline? Can the plane be tiled with tetrads formed from congruent (or similar) tiles? For both questions, the answer is yes. However, one could impose further conditions like symmetry of the tiles or number of vertices given. Not all resulting mathematical problems have been solved yet. However, the examples in this game will answer many of them. Have fun exploring; maybe you can invent a few new tetrads!
List of tetrads shown
Nr comment
1 to 8 tetrads made from 8-ominoes
9 to 10 tetrads made from 9-ominoes
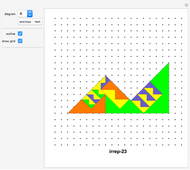
11 to 13 tetrads built from mirror-symmetrical tiles
14, 15 tetrads built from point-symmetrical tiles
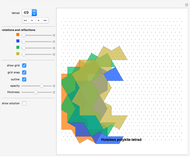
16 to 50 gap-free tetrads (also called holeless tetrads)
The focus in this Demonstration is on holeless tetrads. All known cases of holeless tetrads are presented except one which is made from polycairo tiles.
References
Tetrads number 1 to 8, 11, 13, 14, 16 and 32 were found by George Sicherman.
Tetrad number 28 was found by Frank Rubin.
Tetrads number 18, 29, 33 and 46 were found by Scott Kim.
Juris Čerņenoks found tetrads 44, 45 and 48.
All others are by the author.
Related publications:
- the author's book, A Puzzling Journey to the Reptiles and Related Animals
- the author's Zillions game, "Tetrads"
- problem 684 in The Journal of Recreational Mathematics, 1979
Controls
Control slider "thickness" is for tetrads 37 to 42 and 50 only, since the tiles of these tetrads are only outlined.
Click "show solution" to see the finished tetrad.
Missing case
There is only one holeless tetrad missing here, namely the "polycairo tetrad". This special case is now covered in the Demonstration "Cairo Tilings".
Permanent Citation
"Tetrads"
http://demonstrations.wolfram.com/Tetrads/
Wolfram Demonstrations Project
Published: April 14 2008