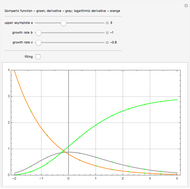
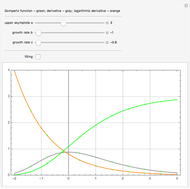
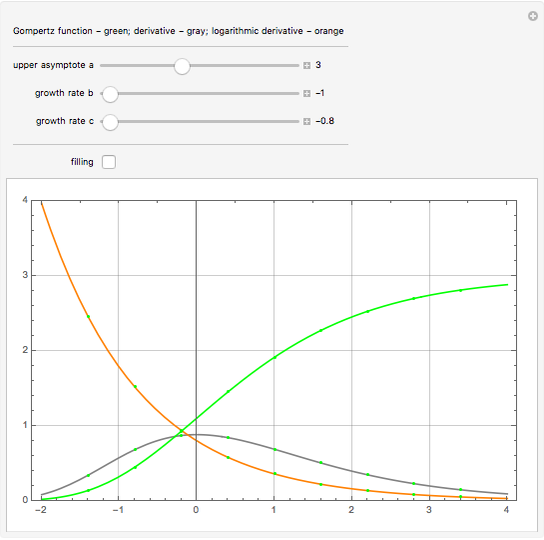
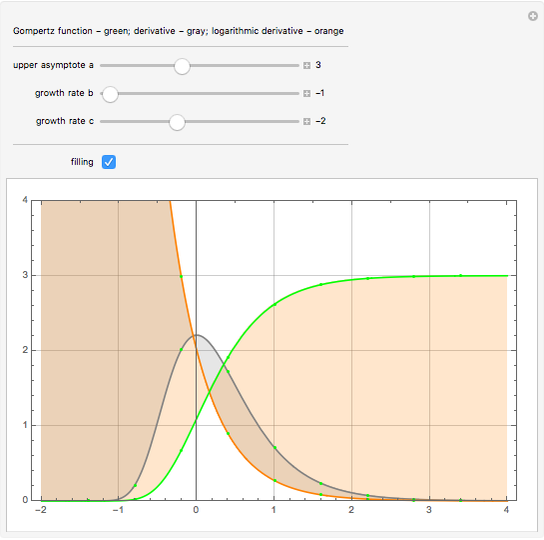
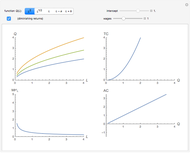
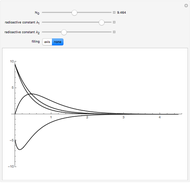
This Gompertz function is defined by or , where is the upper asymptote and and are the negative growth rates. The Gompertz function is a sigmoid function. It is a type of mathematical model for a time series, where growth is slowest at the start and end of a time period. This Demonstration plots the Gompertz function , its derivative, , and the ratio )= .