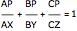Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Intersections of Extended Cevians with Three Circumcircles of Subtriangles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

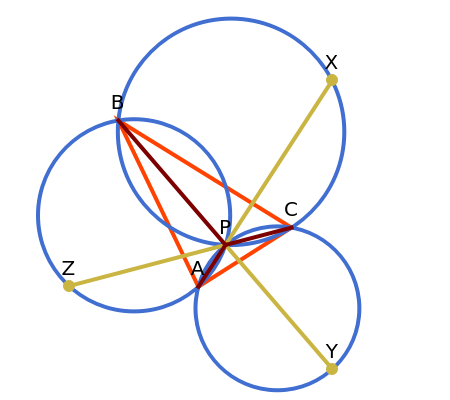
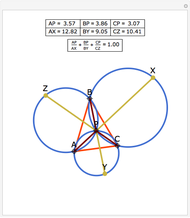
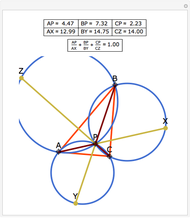
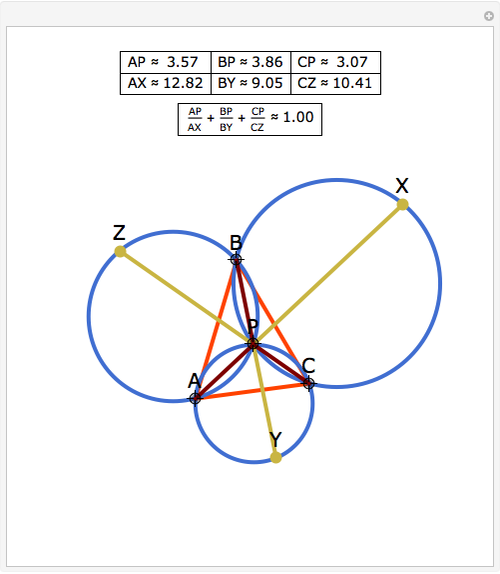
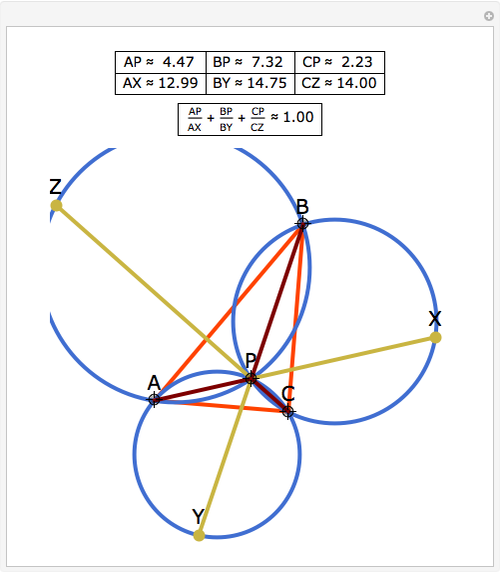
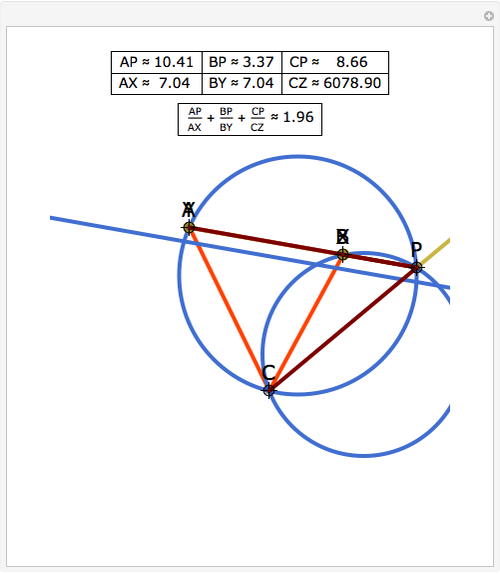
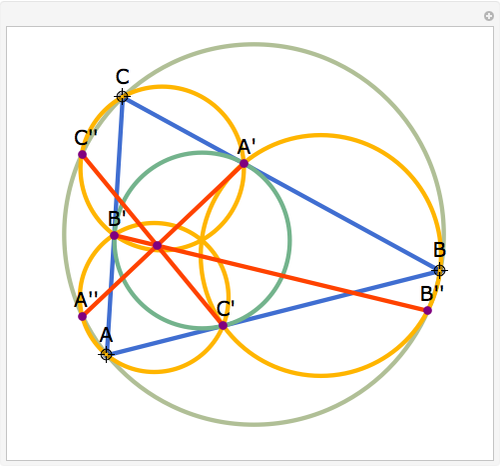
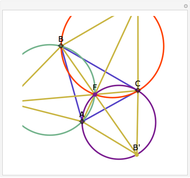
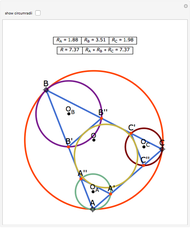
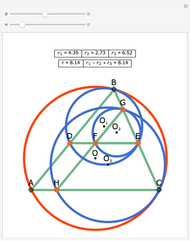
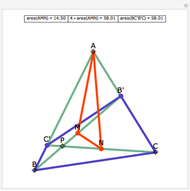
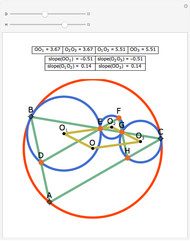
Let P be a point in the interior of the triangle ABC. Draw the three circumscribed circles for the triangles APB, APC, and BPC. Let X, Y, and Z be the intersections (other than P) of the extensions of AP, BP, and CP with the circles opposite A, B, and C. Then:

[more]

.

[less]

Contributed by: Jay Warendorff (March 2011)
After work by: Olexandr Manzjuk
Open content licensed under CC BY-NC-SA

Snapshots

Details

See Ukrainian Journal Contest, Problem 326, by Olexandr Manzjuk.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send