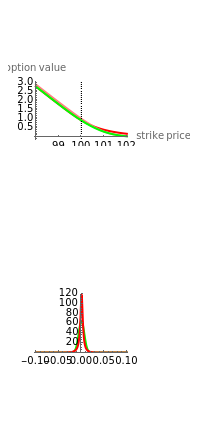
Nonuniqueness of Option Pricing Under the Meixner Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
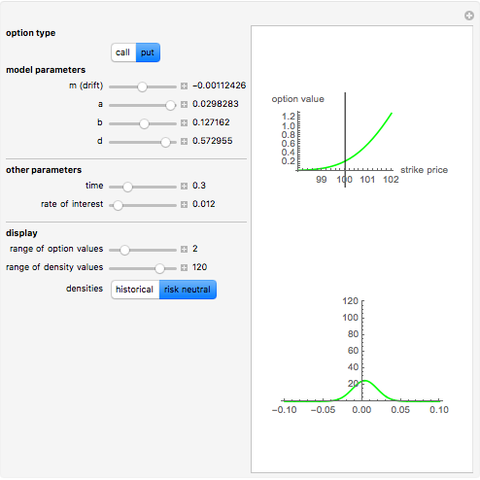
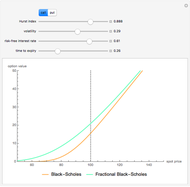
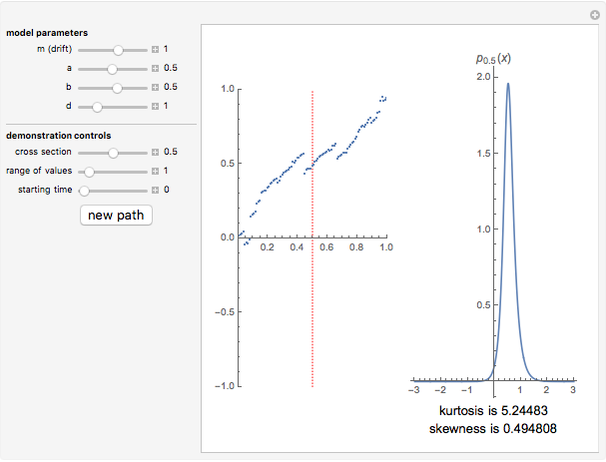
In the classical Black–Scholes model of asset prices, every option has a unique "fair" price; that is, for every price of the underlying asset, there is a unique option price that does not allow arbitrage opportunities. This is no longer true when the Black–Scholes model is replaced by a more realistic model, for example, one in which discontinuous jumps in asset price can occur. This Demonstration shows this for the case where the asset price is modeled by a Meixner process.
[more]
Contributed by: Andrzej Kozlowski (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
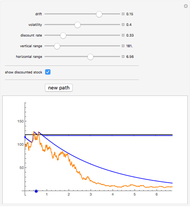
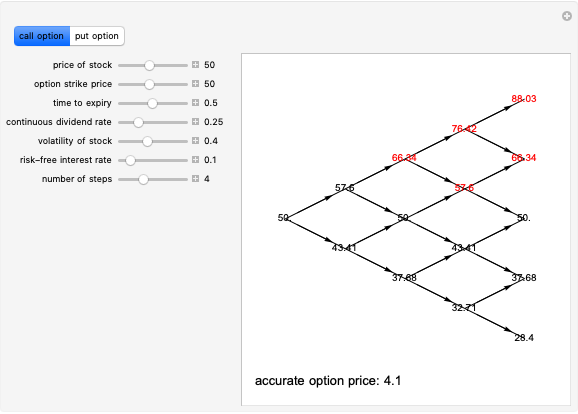
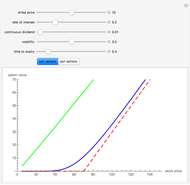
The Black–Scholes model and other one-dimensional diffusion models are examples of complete markets: any option can be perfectly replicated by a self-financing strategy involving the underlying asset and cash. This means that in such models, the price of the underlying parameters and knowledge of the relevant parameters (interest rate and volatility) uniquely determines the "fair" (i.e., arbitrage-free) price of every option. In probabilistic terms, the problem of option pricing reduces to the problem of finding a new probability measure on the space of all possible events, which is equivalent to the real-world measure (in the sense that the sets of impossible events under both measures are the same) but under which the price process is a martingale. In diffusion-based models, there is only one such measure, known as the "equivalent martingale measure".
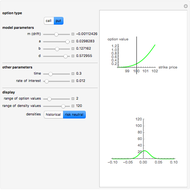
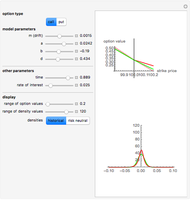
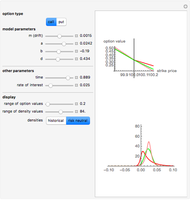
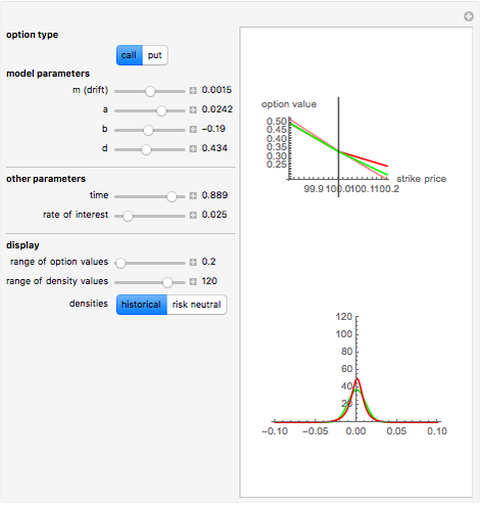
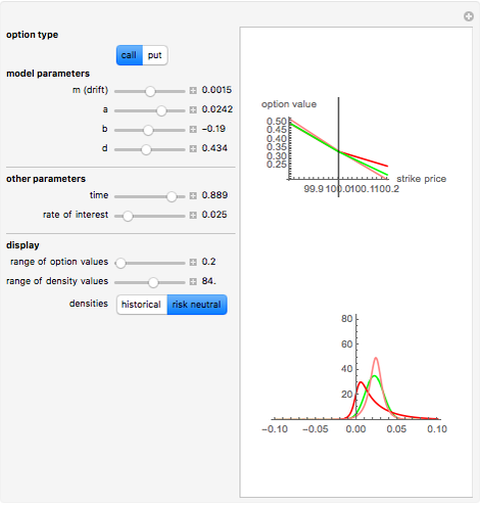
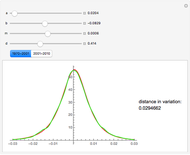
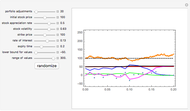
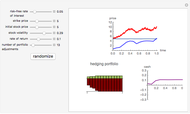
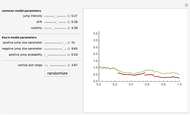
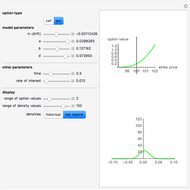
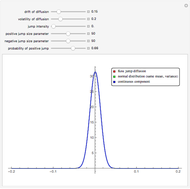
However, models that allow jumps (e.g., models obtained by replacing the Wiener process by another Lévy process) are incomplete: there are infinitely many martingale measures equivalent to the historical (real-world) measure. A choice of any of these measures will give a consistent (arbitrage-free) system of prices for all options sold in the market. Such a measure can be given by specifying the corresponding probability density function, which can then be used to compute prices of options (as expectations with respect to the new measure). Two of the most popular are obtained by means of the so-called Esscher transform (well-known in actuarial mathematics) and by "mean correction", a method analogous to the one used in Black–Scholes pricing. In this Demonstration, we compare the prices obtained by applying both of these methods to models based on the Meixner process (an infinite-activity Lévy process) and display both the historical and equivalent risk-neutral densities. We also compare the prices and the densities with the corresponding Black–Scholes price and density. For certain values of the parameters, it may be difficult to distinguish the graphs of prices or densities of different models. In such cases, you can obtain a clearer view by adjusting either the option price range slider or the range of the graph of densities. This is particularly useful when we want to compare the tails of the distributions (the Meixner densities are both more peaked and have thicker tails than the normal density).
The starting parameters of the Meixner process are obtained by fitting the Meixner distribution to the returns of the S&P 500 index. One of the bookmarks contains parameters obtained by fitting the Meixner distribution to the returns of the Nikkei index.
Reference
[1] W. Schoutens, Lévy Processes in Finance: Pricing Financial Derivatives, New York: John Wiley & Sons, 2003.
Permanent Citation
"Nonuniqueness of Option Pricing Under the Meixner Model"
http://demonstrations.wolfram.com/NonuniquenessOfOptionPricingUnderTheMeixnerModel/
Wolfram Demonstrations Project
Published: August 16 2012