The Seven Bridges of Königsberg

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
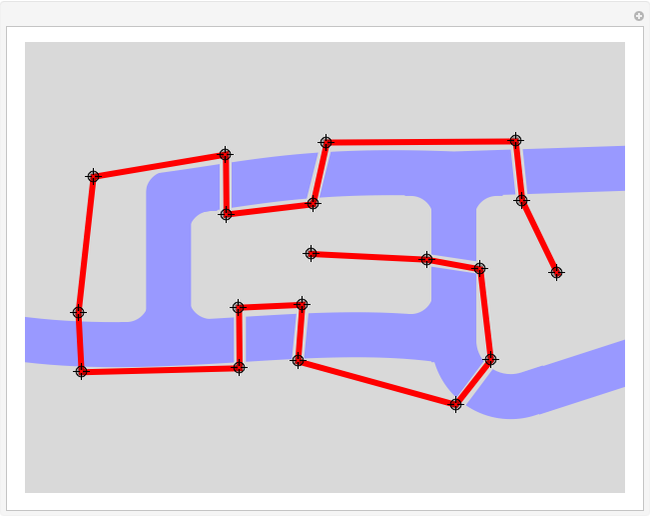
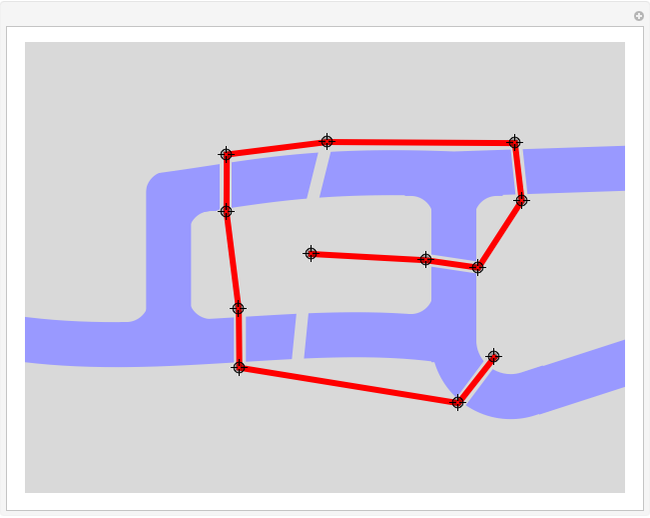
In the 1730s, Leonhard Euler lived in the Prussian city of Königsberg. The Pregel River runs around the center of the city (Kneiphof) and then splits into two parts. The city was then quite prosperous and the volume of commerce justified connections between the separated land masses by seven bridges. A popular problem of the day was to find a continuous path which would cross all seven bridges once and only once.
[more]
Contributed by: S. M. Blinder (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
We apologize for your futile efforts in trying to solve the problem. In fact, Euler proved that no solution exists. It is easy to see why. The four land masses are the north and south shores and the two islands. Any path must arrive at and depart from a land mass via two different bridges (lest one bridge be used twice), so for any legal path to exist, each land mass must be approachable by an even number of bridges.
Euler's more sophisticated treatment can be considered as the beginning of what is now graph theory and, more generally, the entire field of topology.
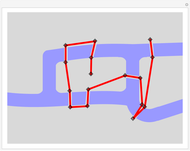
Snapshot 1: an illegal solution since one bridge is crossed twice
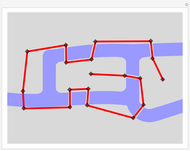
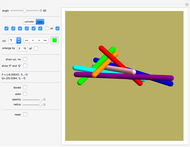
Snapshot 2: adding an eighth bridge can make the problem solvable
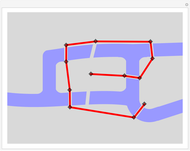
Snapshot 3: with two of the bridges destroyed by bombing in World War II, another solution is possible
Reference
[1] Wikipedia. "Seven Bridges of Königsberg." (Jul 8, 2013) en.wikipedia.org/wiki/Seven_Bridges_of _K % C3 % B6nigsberg.
Permanent Citation
"The Seven Bridges of Königsberg"
http://demonstrations.wolfram.com/TheSevenBridgesOfKoenigsberg/
Wolfram Demonstrations Project
Published: July 15 2013