Three Concyclic Sets of Points Associated with the Orthic Triangle
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
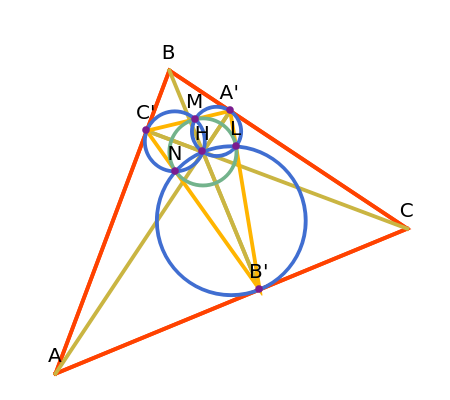
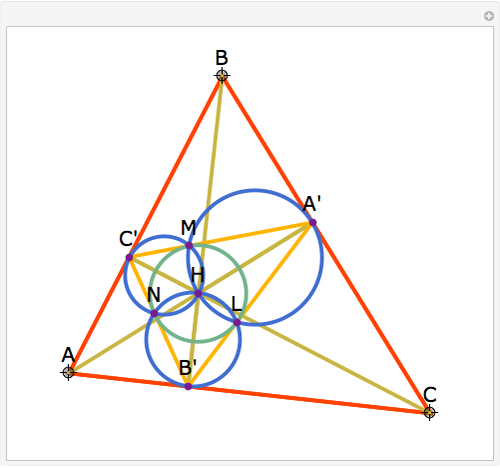
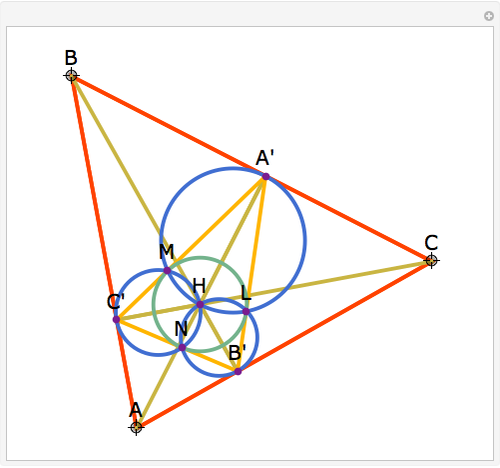
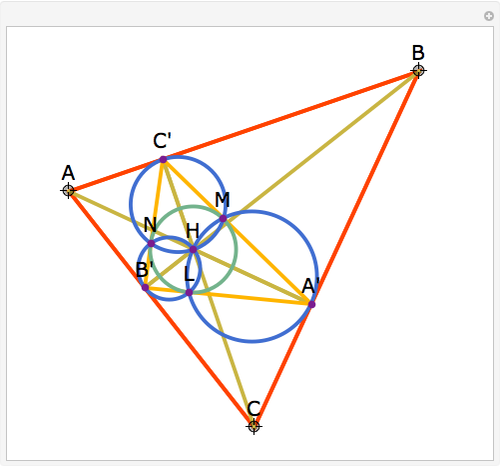
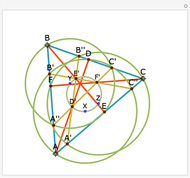
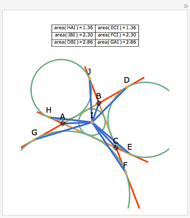
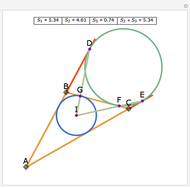
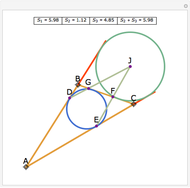
Let ABC be an acute triangle and H its orthocenter. Let A', B', and C' be the feet of the altitudes from A, B, and C. Let L, M, and N be the contact points of the orthic triangle with its incircle with L on A'B', M on A'C', and N on B'C'. Then A', M, H, L are concyclic as are B', L, H, N and C', M, H, N.
Contributed by: Jay Warendorff (March 2011)
After work by: Antonio Gutierrez
Open content licensed under CC BY-NC-SA
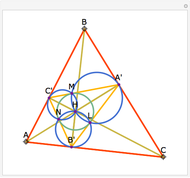
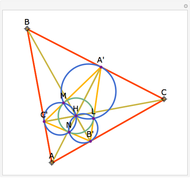
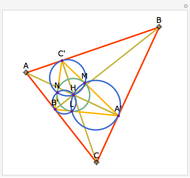
Snapshots
Details
The statement of the theorem is in Problem 136. Orthic Triangle, Altitudes, Orthocenter, Incenter, Perpendicular, Concyclic Points.
Permanent Citation