Value at Risk
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
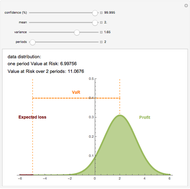
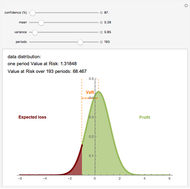
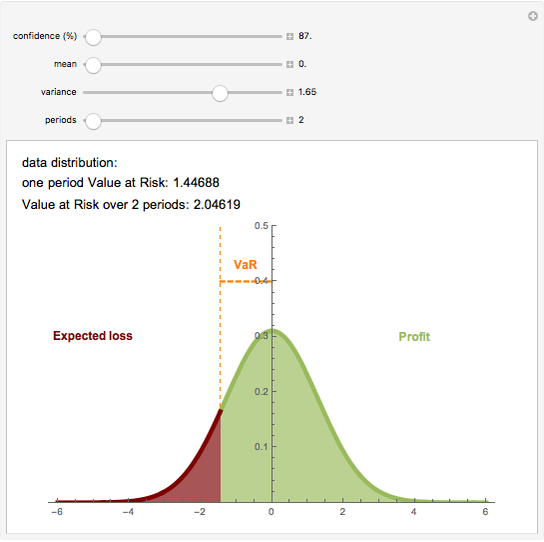
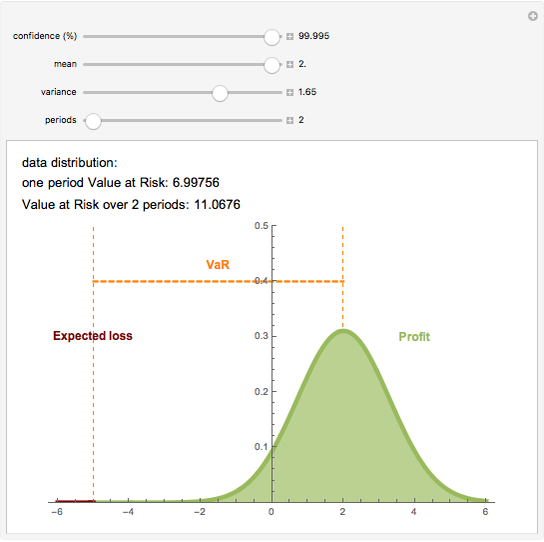
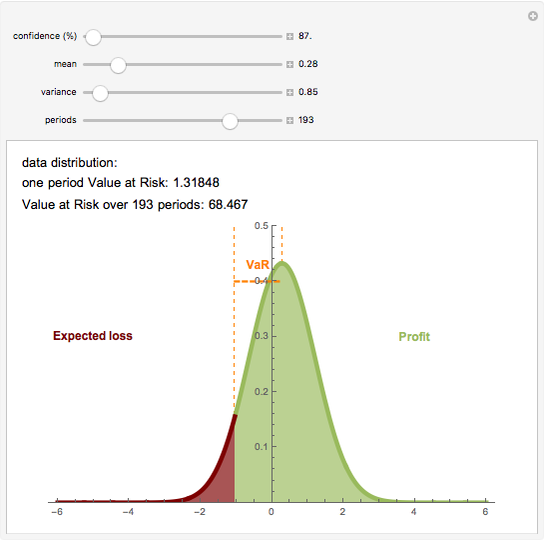
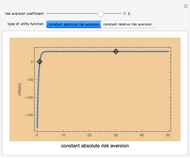
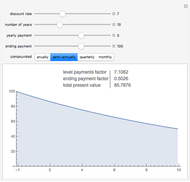
Value at Risk (VaR) and volatility are the most commonly used risk measurements. VaR is easy to calculate and can be used in many fields. VaR is defined as the sum of the data mean and the product of data volatility and an appropriate quantile of 
distribution. This quantile indicates the confidence level of the result. This interpretation of VaR assumes that the data is normally distributed; however the calculation works in any setting.
Contributed by: Gergely Nagy (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Interpretation of VaR
Suppose the VaR over a one-day holding period is 1000 (the VaR is expressed as an absolute number amount) at a confidence level of 99%. That means that 99% of the time (i.e., 99 out of 100 trading days), a maximum loss of 1000 is expected once and the second largest loss in 100 days is expected to be no more than 1000. For the worst 1% of days the minimum loss of 1000 is expected.
The VaR for a 
-long period (e.g. days) is calculated as the product of one period VaR (with mean zero) and 
, where 
is the data mean.
Permanent Citation
Bootstrapping to Compute Value-at-Risk Standard Errors
Jeff Hamrick
Risk Premiums
John Horton
Risk, Ownership, and Control
Roger J. Brown
Constant Risk Aversion Utility Functions
Seth J. Chandler
Present Value Calculator
Craig Bauling
Options: Time Value
Peter Falloon
Future Value Calculator
Sarah Lichtblau
Net Present Value
Fiona Maclachlan
Discounted Present Value
Jason Cawley
Expanded Fermi Solution for Risk Assessment
Mark D. Normand, Micha Peleg and Joseph Horowitz
