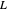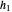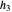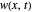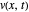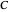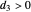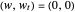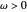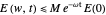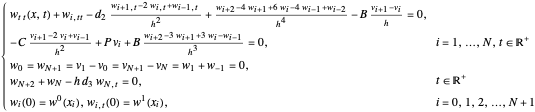Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Vibration Suppression on a Hinged Three-Layer Sandwich Beam

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

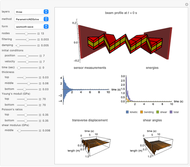
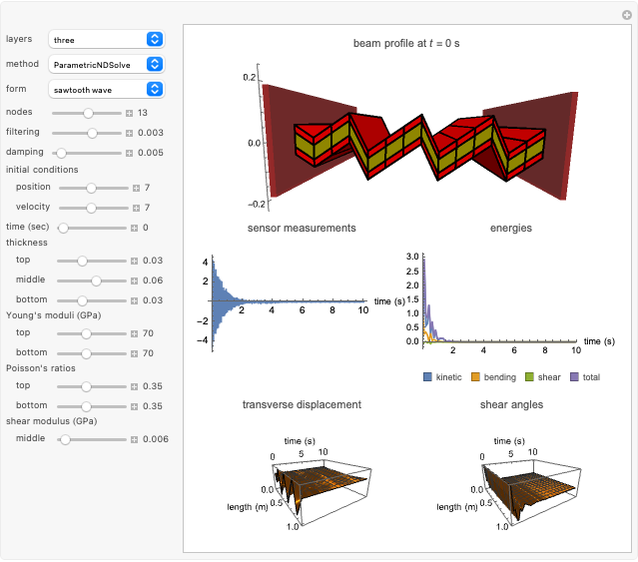
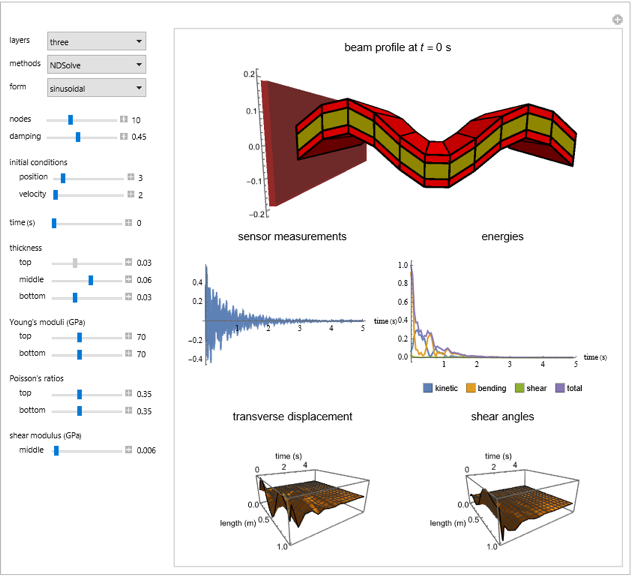
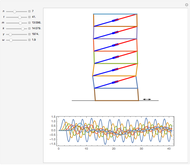
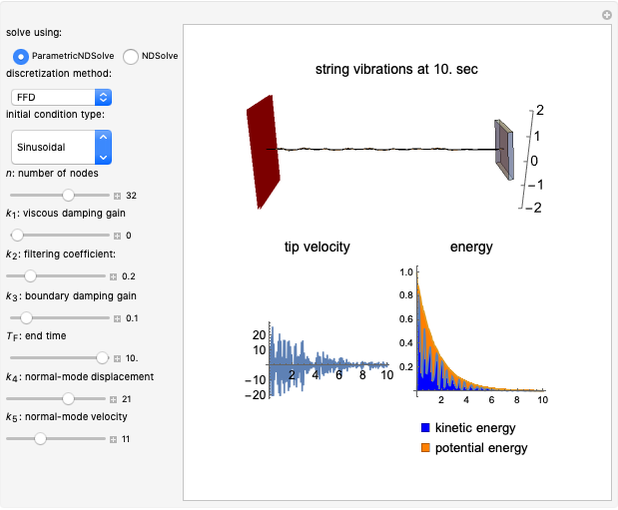
This Demonstration considers boundary controlled vibrations on a hinged three-layer sandwich beam, consisting of a viscoelastic middle layer sandwiched (and perfectly bonded) between two outer elastic/piezoelectric layers. Outer and middle layers are modeled by the Euler–Bernoulli and the Mindlin–Timoshenko small displacement assumptions, respectively [5]. The outer layers are resistant to transverse shear of the filaments, while the middle viscoelastic layer allows transverse shear. Therefore, the only coupling across the layers is due to the shear of the middle viscoelastic layer. The layers, even though bonded, can move longitudinally during the motion. To suppress vibration, a sensor/controller is placed at the tip of the beam.

[more]

Consider the layers of the sandwich beam of length and thicknesses , , from the bottom to the top. The equations of motion follow the widely used Mead–Marcus-type beam equations, which are described by the following partial differential equation (PDE):

(1)

Here, represents the overall bending of the beam, represents the shear angle of the middle layer and , , represent positive physical constants of shear modulus, Young's moduli, Poisson's ratios and layer thicknesses. Note that with refers to the boundary damping measurements fed back to the closed-loop dynamics. (For more details about constants and the modeling assumptions, see [4, 5]).

The energy

of the solutions ) of (1) are known to decay to the equilibrium state exponentially fast. Thus, there exists , such that (see [6] and the references therein).

As (1) is approximated by finite differences [1, 7], the solutions of the reduced system do not retain exponential stability uniformly as the mesh parameter . Moreover, the reduced model fails to accurately represent the dynamics of (1).

To prevent this discrepancy, the solutions are "indirectly" filtered by adding a viscosity term with to the first equation in (1). As a side note, (1) with cantilevered boundary conditions is handled in [2] without the need for any numerical filtering.

(2)

[less]

Contributed by: Ahmet Kaan Aydin, Matthew Poynter and Ahmet Özkan Özer (January 2023)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The PDE model (1) is approximated by finite differences. Let the mesh parameter be 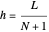, where is the number of nodes in the uniform discretization in space variable , with 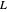set equal to 1 for simplicity. Now, the nodes of the discretization are 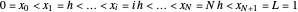. To handle the second-order boundary conditions, two fictitious points 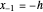, are also introduced.

Let 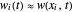, 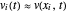describe the uniform bending of the overall sandwich beam and transverse shear angle of the middle layer on the beam, respectively. The following model reduction of (1) is proposed

where the viscosity term 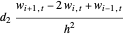, called the indirect filtering term corresponding to 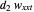with the filtering parameter 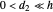is added to fix the discrepancy. The model with 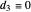is shown to be uniformly observable as 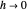with the sensor measurement , and therefore, the solutions of (2) are exponentially stable, mimicking (1) (see [1, 3, 7] and the references therein).

The initial conditions can be chosen in different forms with an amplitude of 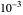. Material constants and thicknesses of each layer can be determined individually. In order to better visualize the transverse displacements in the beam profile plot, 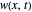is scaled up. The single-layer beam model is also shown, which is equivalent to (2) with 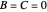(see [7]). As a side note, the same filtering method is successfully implemented for the boundary-damped wave equation (see the Related Links).

This material is based upon work supported by the National Science Foundation under Cooperative Agreement No. 1849213.

References

[1] A. K. Aydin, "Robust Sensor Design for the Novel Reduced Model of the Mead-Marcus Sandwich Beam Equation," M.Sc. thesis, Department of Mathematics, Western Kentucky University, Bowling Green, KY, 2022. digitalcommons.wku.edu/theses/3603.

[2] A. K. Aydin, M. Poynter and A. Ö. Özer, "Feedback Sensor Design for a Cantilevered Three-Layer Sandwich Beam," Wolfram Demonstrations Project. (Dec 13, 2022) demonstrations.wolfram.com/FeedbackSensorDesignForACantileveredThreeLayerSandwichBeam.

[3] I. F. Bugariu, S. Micu and I. Roven\:0163a, "Approximation of the Controls for the Beam Equation with Vanishing Viscosity," Mathematics of Computation, 85, 2016 pp. 2259–2303. doi:10.1090/mcom/3064.

[4] S. W. Hansen, "Several Related Models for Multilayer Sandwich Plates," Mathematical Models and Methods in Applied Sciences, 14(8), 2004 pp. 1103–1132. doi:10.1142/S0218202504003568.

[5] D. J. Mead and S. Markus, "The Forced Vibration of a Three-Layer, Damped Sandwich Beam with Arbitrary Boundary Conditions," Journal of Sound and Vibration, 10(2), 1969 pp. 163–175. doi:10.1016/0022-460X(69)90193-X.

[6] A. Ö. Özer, "Dynamic and Electrostatic Modeling for a Piezoelectric Smart Composite and Related Stabilization Results," Evolution Equations and Control Theory, 7(4), 2018 pp. 639–668. doi:10.3934/eect.2018031.

[7] A. Ö. Özer and A. K. Aydin, "Uniform Boundary Observability of Filtered Finite Difference Approximations of a Mead–Marcus Sandwich Beam Equation with Only One Boundary Observation," forthcoming in 2022 IEEE 61st Conference on Decision and Control (CDC), Cancún, Mexico, 2022.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send