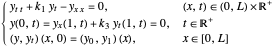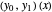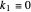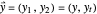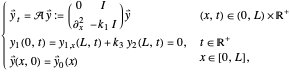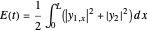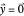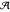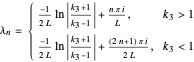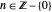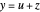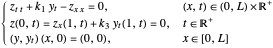Stabilization of the Wave Equation by Direct Fourier Filtering

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
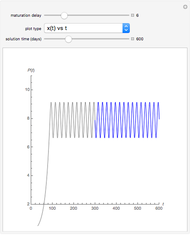
This Demonstration shows approximated solutions of the one-dimensional boundary-controlled wave equation on the domain 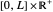 , with the following PDE model
, with the following PDE model
Authored by: Jacob Walterman, Ahmet Kaan Aydin, Matthew Poynter, Ahmet Ozkan Ozer (January 2023)
Open content licensed under CC BY-NC-SA
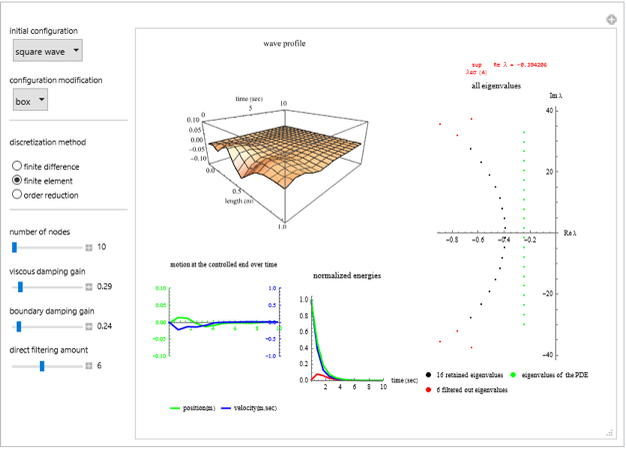
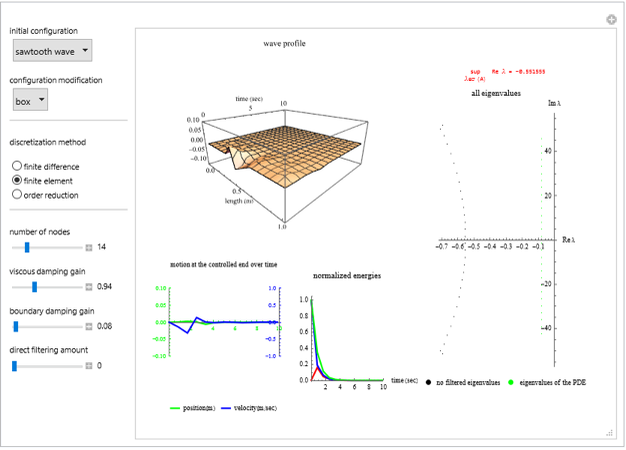
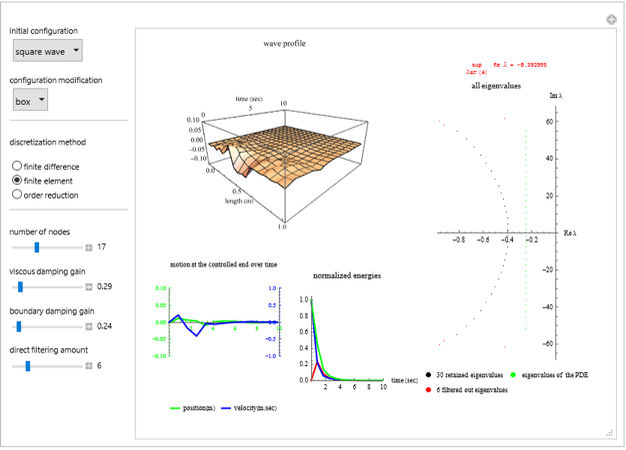
Snapshots
Details
Three approximation techniques for (1) are implemented. For each technique, let the mesh parameter be 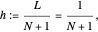 where
where 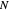 is the number of nodes in the uniform discretization in space variable
is the number of nodes in the uniform discretization in space variable  , and
, and 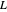 is taken to be 1 for simplicity. Now, we have the following nodes:
is taken to be 1 for simplicity. Now, we have the following nodes:
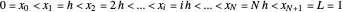 .
.
Consider the matrices
 ,
,
 ,
,
 ,
,
 .
.
As the model (1) is discretized in the spatial variable  by the standard finite differences or finite elements (with linear splines) for the discretization above, in contrast to (3), the real parts of the eigenvalues of the reduced system matrix
by the standard finite differences or finite elements (with linear splines) for the discretization above, in contrast to (3), the real parts of the eigenvalues of the reduced system matrix 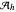 converge to zero as
converge to zero as 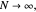 which is referred to as a lack of exponential stability [1, 2]. This means that the finite-difference or finite-element approximations might not accurately represent the dynamics of (1). To prevent this, the so-called direct Fourier Filtering Technique [3, 4] is adopted.
which is referred to as a lack of exponential stability [1, 2]. This means that the finite-difference or finite-element approximations might not accurately represent the dynamics of (1). To prevent this, the so-called direct Fourier Filtering Technique [3, 4] is adopted.
Now let

be the approximations at each node 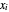 corresponding to the PDEs (1), (4) and (5), respectively. Then, for
corresponding to the PDEs (1), (4) and (5), respectively. Then, for 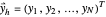 ,
, 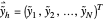 ,
,  ,
, 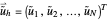 ,
, 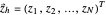 ,
, 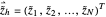 , (1), (4) and (5) are formed into the following first-order formulations:
, (1), (4) and (5) are formed into the following first-order formulations:
Filtered Finite Differences (FFD)
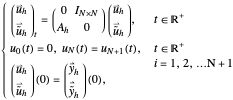
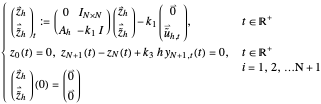
Filtered Finite Elements (FFE)

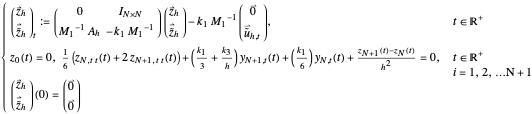
In both FFD and FFE, the real parts of the high-frequency eigenvalues of the system matrices tend to zero, unlike the eigenvalues (3) of (1). To avoid this discrepancy, the spurious high-frequency eigenvalues must be filtered by the Fourier filtering. Let 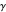 be the Fourier filtering parameter. For a choice of
be the Fourier filtering parameter. For a choice of  (
(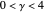 for FFD and
for FFD and  for FFE), consider solutions
for FFE), consider solutions 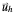 in the filtered solutions space
in the filtered solutions space 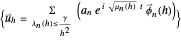 where
where 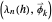 are the eigensystems for the matrices
are the eigensystems for the matrices 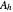 and
and  , respectively.
, respectively.
Since the filtering parameter 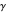 is chosen closer to zero, too many high-frequency eigenvalues are filtered out. As the filtering parameter is chosen closer to 4 (for FFD) and 12 (for FFE), almost all eigenvalues are retained, with just a few high-frequency eigenvalues filtered out.
is chosen closer to zero, too many high-frequency eigenvalues are filtered out. As the filtering parameter is chosen closer to 4 (for FFD) and 12 (for FFE), almost all eigenvalues are retained, with just a few high-frequency eigenvalues filtered out.
We also provide another recently introduced technique just for comparison [5]. Note that the following model does not need any filtering:
Order-Reduced (Unfiltered) Finite Differences (ORUFD)
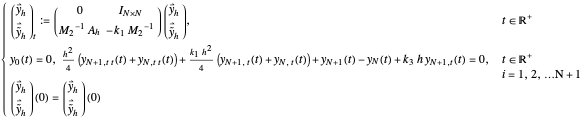 .
.
The initial conditions 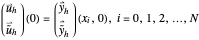 can be chosen in the form of sinusoidal, pinch, box, square-wave, triangular-wave, sawtooth-wave.
can be chosen in the form of sinusoidal, pinch, box, square-wave, triangular-wave, sawtooth-wave.
Note that the indirect filtering technique, based on adding a viscosity term to (1), is successfully used for the wave equation [6, 7] for the comparison and for the Rayleigh beam equation [8]. The implementation of filtering in [6] is not achieved by the decomposition technique as in this work but in an ad-hoc fashion.
This material is based upon the work supported by the National Science Foundation under Cooperative Agreement No. 1849213. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
References
[1] G. H. Peichl and C. Wang, "Asymptotic Analysis of Stabilizability of a Control System for a Discretized Boundary Damped Wave Equation", Numerical Functional Analysis and Optimization, 19(1–[3]), 1998 pp. 91–113. doi:10.1080/01630569808816817.
[2] H. T. Banks, K. Ito and C. Wang, "Exponentially Stable Approximations of Weakly Damped Wave Equations," Estimation and Control of Distributed Parameter Systems (W. Desch, F. Kappel and K. Kunisch, eds.), Basel: Birkhäuser, 1991 pp. 1–33. doi:10.1007/978-3-0348-6418-3_1.
[3] H. El Boujaoui, H. Bouslous and L. Maniar, "Boundary Stabilization for  Semi-discrete Wave Equation by Filtering Technique," Bulletin of TICMI, 17(1), 2013 pp. 1–18. emis.de/journals/TICMI/vol17_1/boujaoui.pdf.
Semi-discrete Wave Equation by Filtering Technique," Bulletin of TICMI, 17(1), 2013 pp. 1–18. emis.de/journals/TICMI/vol17_1/boujaoui.pdf.
[4] J. A. Infante and, E. Zuazua, "Boundary Observability for the Space Semi-discretizations of the 1-D Wave Equation," ESAIM, 33(2), 1999, pp. 407–438. doi: 10.1051/m2an:1999123.
[5] J. Liu and B.-Z. Guo, "A New Semidiscretized Order Reduction Finite Difference Scheme for Uniform Approximation of One-Dimensional Wave Equation," SIAM Journal on Control and Optimization, 58(4), 2020 pp. 2256–2287. doi:10.1137/19M1246535.
[6] M. Poynter, L. Stewart, A. K. Aydin and A. Ö. Özer. "Boundary-Feedback Control of Vibrations on a String with and without Filtering" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/BoundaryFeedbackControlOfVibrationsOnAStringWithAndWithoutFi.
[7] D. Price, E. Moore and A. Ö. Özer. "Boundary Control of a 1D Wave Equation by the Filtered Finite-Difference Method" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/BoundaryControlOfA1DWaveEquationByTheFilteredFiniteDifferenc.
[8] A. Ö. Özer, "Uniform Boundary Observability of Semi-discrete Finite Difference Approximations of a Rayleigh Beam Equation with Only One Boundary Observation," in 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 2019, Piscataway, NJ: IEEE, 2019 pp. 7708–7713. doi:10.1109/CDC40024.2019.9028954.
Permanent Citation