Pisot, Salem and Cyclotomic Polynomials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
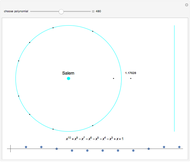
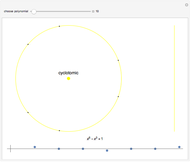
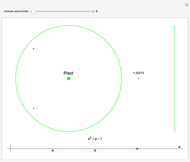
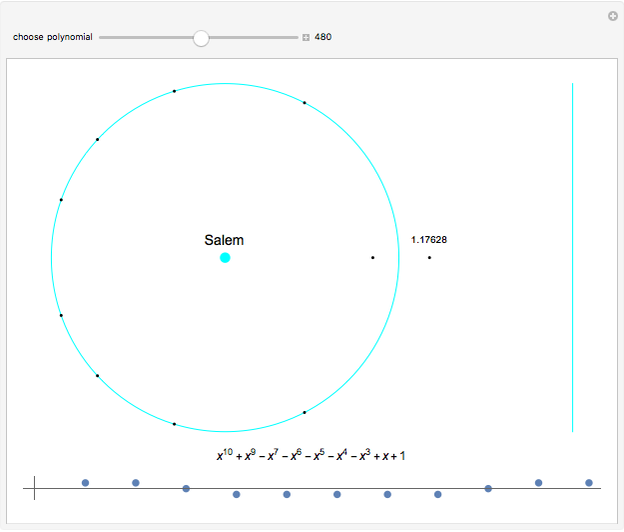
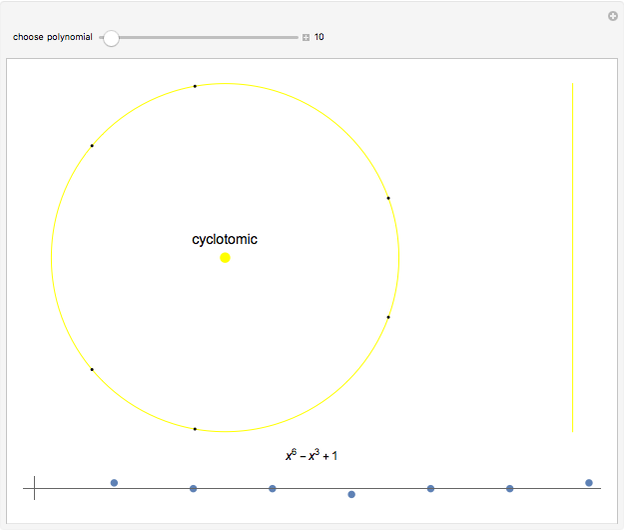
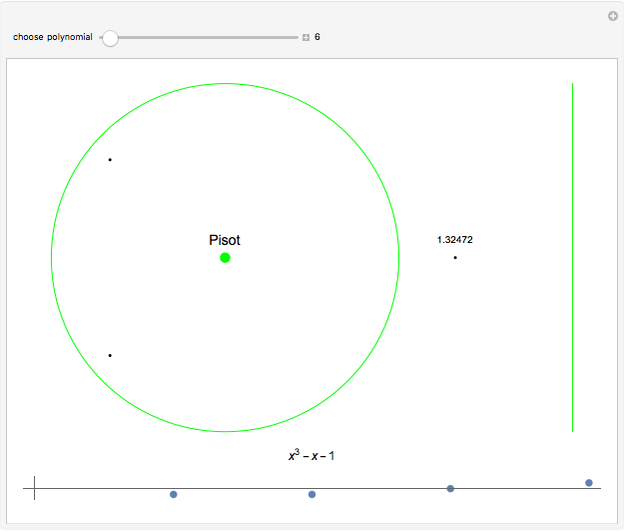
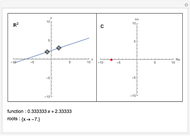
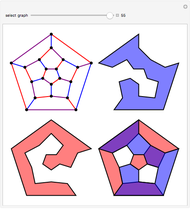
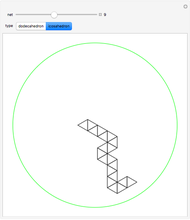
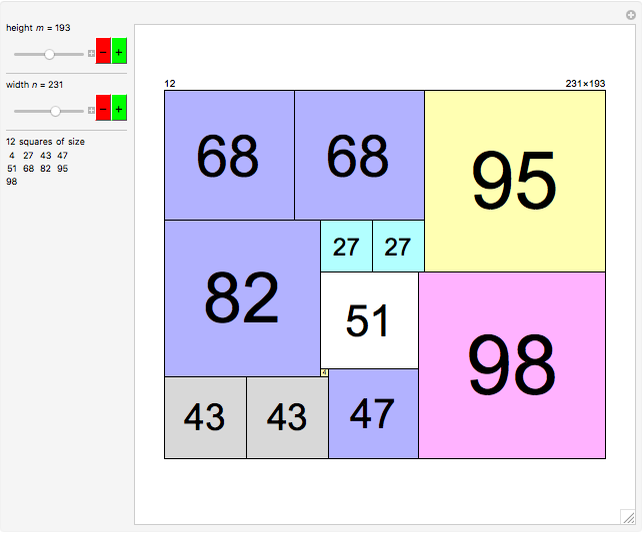
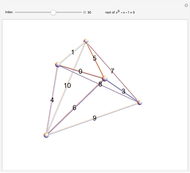
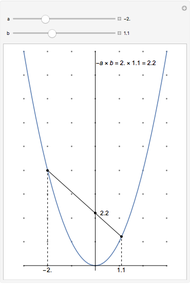
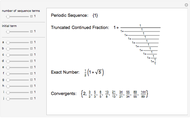
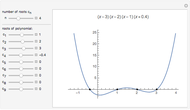
Consider the polynomial  . The first coefficient is 1, making this, by definition, a monic polynomial. Also by definition, the roots of a monic polynomial are called algebraic integers. The polynomial is irreducible, meaning that it cannot be factored into a product of polynomials with integer coefficients. The highest power is 3, so by the fundamental theorem of algebra, the equation
. The first coefficient is 1, making this, by definition, a monic polynomial. Also by definition, the roots of a monic polynomial are called algebraic integers. The polynomial is irreducible, meaning that it cannot be factored into a product of polynomials with integer coefficients. The highest power is 3, so by the fundamental theorem of algebra, the equation  has exactly three complex roots, counting possible multiplicities. Some irreducible monic polynomials with integer coefficients have special names when their roots have certain properties.
has exactly three complex roots, counting possible multiplicities. Some irreducible monic polynomials with integer coefficients have special names when their roots have certain properties.
Contributed by: Ed Pegg Jr (October 2013)
Open content licensed under CC BY-NC-SA
Details
Reference
[1] M. Mossinghoff. "Small Salem Numbers." (Sep 24, 2018) www.cecm.sfu.ca/~mjm/Lehmer/lists/SalemList.html.
Snapshots
Permanent Citation