2D Analog for Coulomb Degeneracies

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
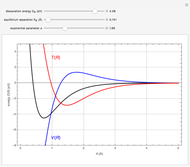
It is a remarkable fact that the nonrelativistic Coulomb (hydrogenlike atom) have sets of degenerate eigenfunctions (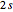 ,
,  ),
), 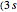 ,
,  ,
,  ), and so on, whose members can exhibit completely different geometrical shapes. It was first shown by Vladimir Fock in 1935 that the Coulomb problem has the same energy spectrum as a free particle moving on the surface of a four-dimensional hypersphere. Thus the bound states of the hydrogen atom exhibit the same
), and so on, whose members can exhibit completely different geometrical shapes. It was first shown by Vladimir Fock in 1935 that the Coulomb problem has the same energy spectrum as a free particle moving on the surface of a four-dimensional hypersphere. Thus the bound states of the hydrogen atom exhibit the same  symmetry as rotations in four dimensions. For the physical three-dimensional problem, this is a "hidden symmetry", which can be attributed to the existence of an additional constant of the motion—the Runge–Lenz vector. In principle, the symmetry can be exhibited by stereographic projection of degenerate hyperspherical harmonics onto a three-dimensional space.
symmetry as rotations in four dimensions. For the physical three-dimensional problem, this is a "hidden symmetry", which can be attributed to the existence of an additional constant of the motion—the Runge–Lenz vector. In principle, the symmetry can be exhibited by stereographic projection of degenerate hyperspherical harmonics onto a three-dimensional space.
Contributed by: S. M. Blinder (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
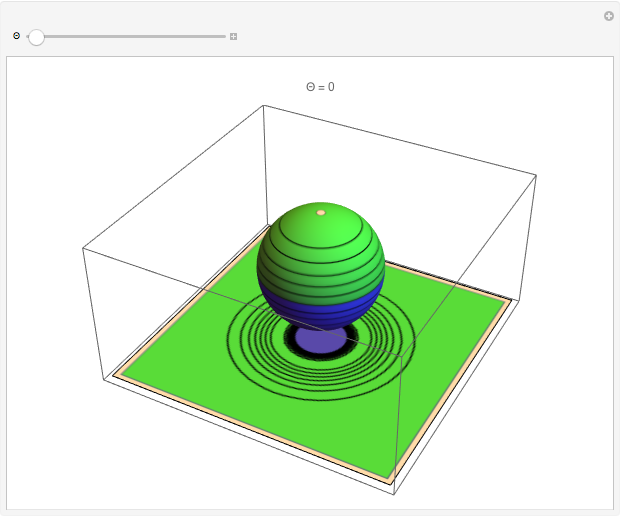
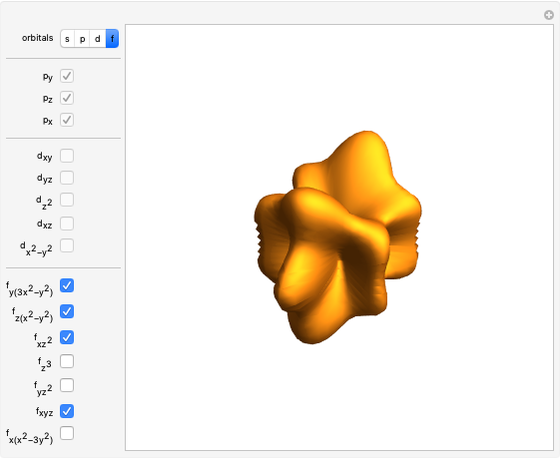
Snapshot 1:  : 2
: 2 -orbital
-orbital
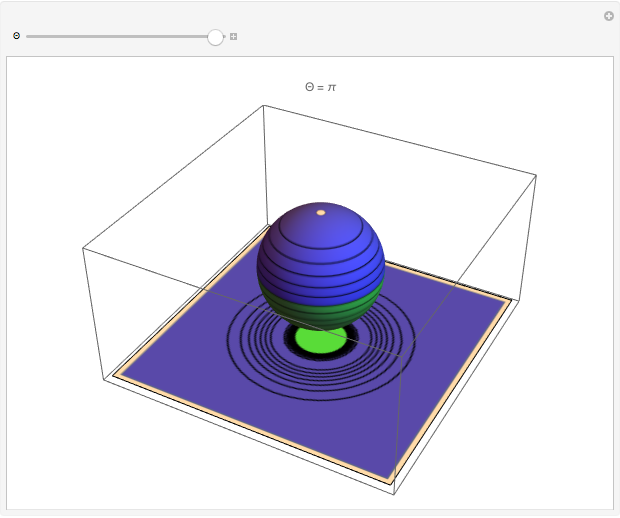
Snapshot 2:  : 2
: 2 -orbital with opposite phase
-orbital with opposite phase
Snapshot 3:  :
: 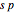 -hybrid orbital
-hybrid orbital
Thumbnail shows 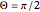 : 2
: 2 -orbital.
-orbital.
Reference
[1] P. W. Atkins, Quanta: A Handbook of Concepts, 2nd ed., Oxford: Oxford University Press, 1991 pp. 80–82.
Permanent Citation