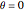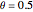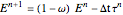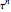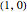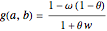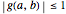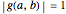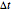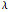If 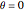 , one recovers the explicit Euler integration scheme.
, one recovers the explicit Euler integration scheme.
If  , one recovers the implicit Euler integration scheme.
, one recovers the implicit Euler integration scheme.
If 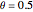 , one recovers the Crank–Nicholson integration scheme.
, one recovers the Crank–Nicholson integration scheme.
Absolute stability means that the global error does not grow without bound.
Absolute stability of the numerical integration method requires the following condition:
 , where the dimensionless time step is
, where the dimensionless time step is  .
.
Consider the Euler integration scheme (i.e., 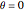 ); the global error,
); the global error,  , satisfies
, satisfies 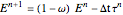 , where
, where 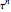 is the local truncation error at time step
is the local truncation error at time step  . This equation reveals the origin of exponential growth in the global error. Indeed, at each time step the global error is multiplied by
. This equation reveals the origin of exponential growth in the global error. Indeed, at each time step the global error is multiplied by  . If
. If  is outside the disk with center at
is outside the disk with center at 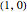 of radius 1, the global error will grow out of bounds and the numerical method will fail to give an accurate solution of the differential equation. Thus, the choice of the time step that gives good solutions is restricted to a specific domain and the method is not absolutely stable.
of radius 1, the global error will grow out of bounds and the numerical method will fail to give an accurate solution of the differential equation. Thus, the choice of the time step that gives good solutions is restricted to a specific domain and the method is not absolutely stable.
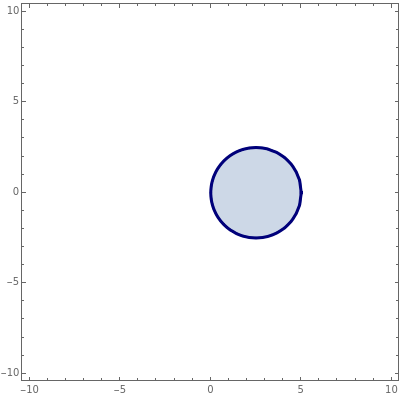
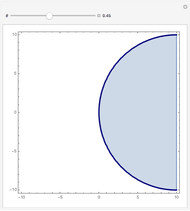
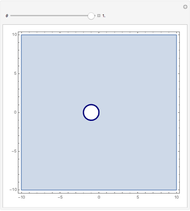
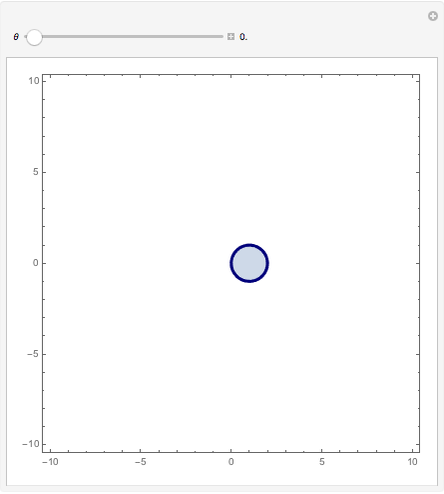
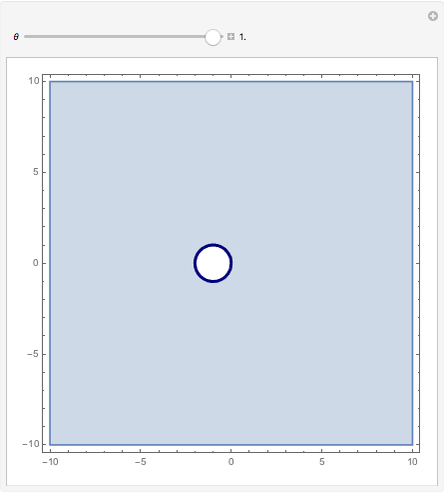
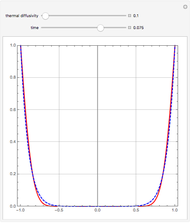
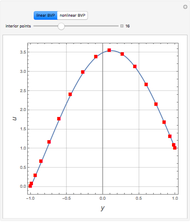
The present Demonstration shows the region plot in the  plane for user-set values of
plane for user-set values of  . With
. With 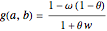 , the light blue region corresponds to
, the light blue region corresponds to 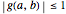 and the blue curve is where
and the blue curve is where 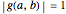 . Thus the light blue region represents choices of
. Thus the light blue region represents choices of 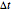 that give absolute stability.
that give absolute stability.
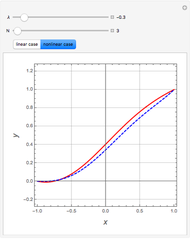
If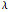 is real, one can conclude that the explicit Euler method is not absolutely stable, while both the implicit Euler and Crank–Nicholson methods are absolutely stable.
is real, one can conclude that the explicit Euler method is not absolutely stable, while both the implicit Euler and Crank–Nicholson methods are absolutely stable.
[less]

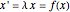 , where
, where 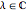 , and the integration scheme
, and the integration scheme 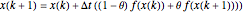 .
.