An Example of the Bolyai-Gerwien Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
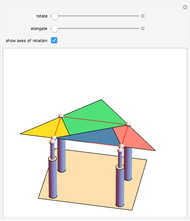
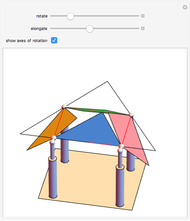
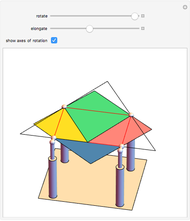
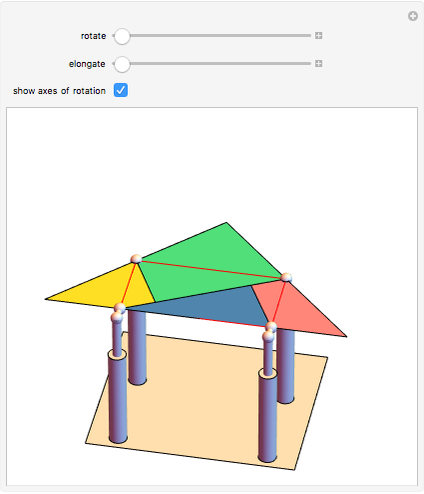
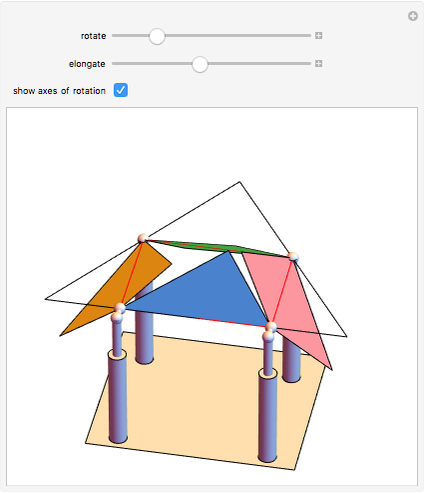
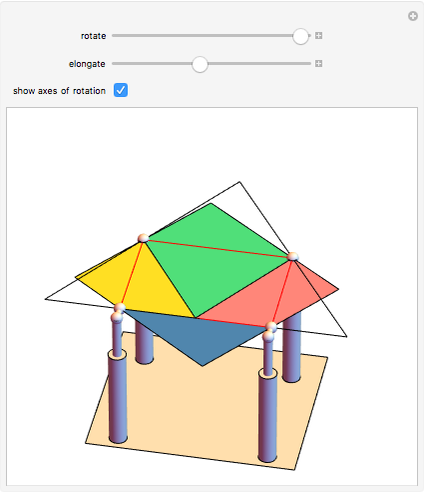
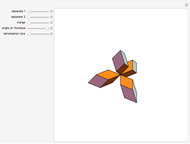
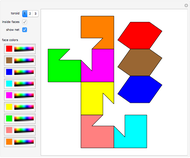
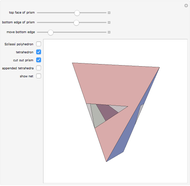
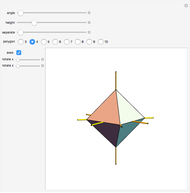
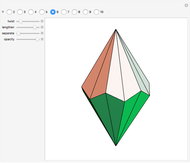
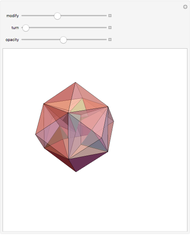
This conceptual design can be used to demonstrate the Bolyai–Gerwien theorem in the case of triangles and rectangles. A triangle is cut into four pieces that can be rotated to form a rectangle. (Henry Dudeney published this as a plane rearrangement puzzle in 1902.)
Contributed by: Sándor Kabai, Ferenc Holló Szabó, and Lajos Szilassi (February 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Bolyai–Gerwien Theorem says that a polygon can be cut into a finite number of triangles that can be reassembled to form any other polygon having the same area. In other words: if two polygons have the same area, then they are equidecomposable (scissor-equivalent). Farkas Bolyai conjectured this in the 1790s and William Wallace proved it in 1808. Unaware of this, Paul Gerwien proved it again in 1833, and then Bolyai, unaware of both earlier results, gave another proof in 1835.
Permanent Citation
"An Example of the Bolyai-Gerwien Theorem"
http://demonstrations.wolfram.com/AnExampleOfTheBolyaiGerwienTheorem/
Wolfram Demonstrations Project
Published: February 26 2008