Japanese Theorem for Cyclic Polygons
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
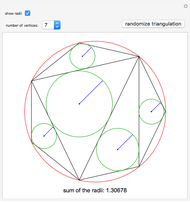
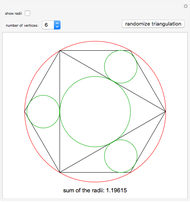
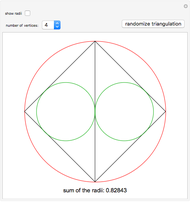
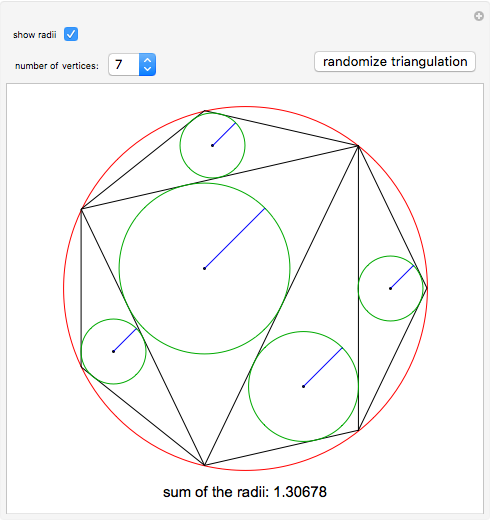
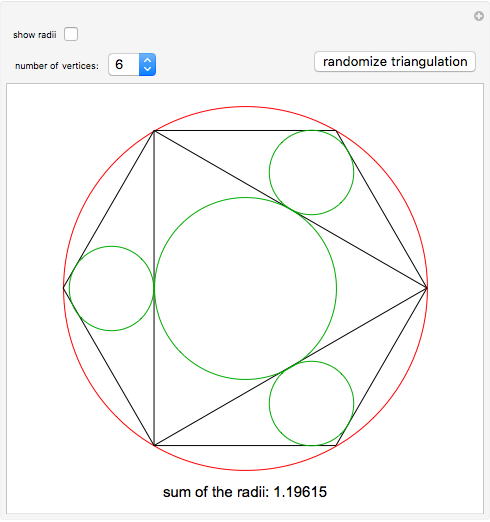
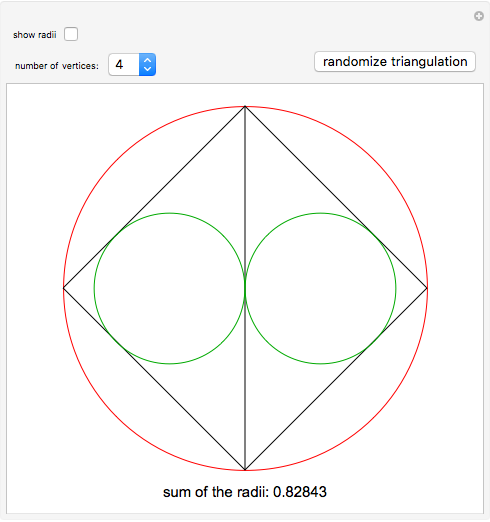
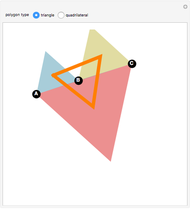
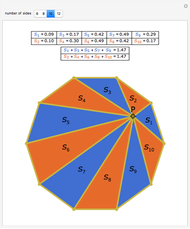
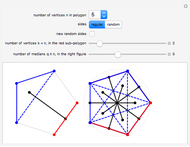
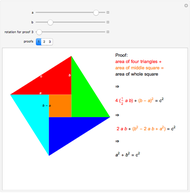
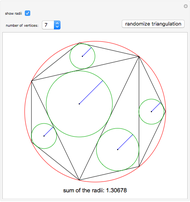
The Japanese theorem for cyclic polygons states that no matter how a cyclic convex polygon is triangulated, the sum of the inradii of the triangles remains constant. This Demonstration shows random triangulations of regular polygons inscribed in a unit circle and the sum of the inradii of the triangles.
Contributed by: David Kang Myung Yang (September 2014)
(Mathematica Summer Camp 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Japanese Theorem for Cyclic Polygons"
http://demonstrations.wolfram.com/JapaneseTheoremForCyclicPolygons/
Wolfram Demonstrations Project
Published: September 2 2014
Nested Polygon Disks
Michael Schreiber
Signed Area of a Polygon
Bruce Atwood (Beloit College) and Stan Wagon (Macalester College)
Napoleon's and van Aubel's Theorems
Robert Dickau
Total Areas of Alternating Subtriangles in a Regular Polygon with 2n Sides
Jay Warendorff
Median Theorem for Polygons
Roger B. Kirchner
Three Proofs of the Pythagorean Theorem
Sid Venkatraman
Approximating Pi with Inscribed Polygons
Rob Morris
Angle and Length Measurement of a Polygon
Faisal Whelpley
Point in Triangle
Michael John Twardos
Drawing a Triangle
Michael Trott
