Approximating Pi with Inscribed Polygons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
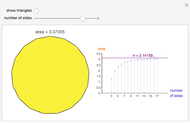
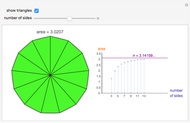
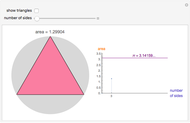
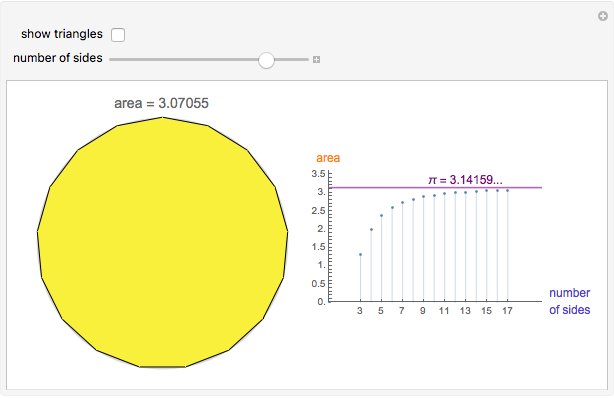
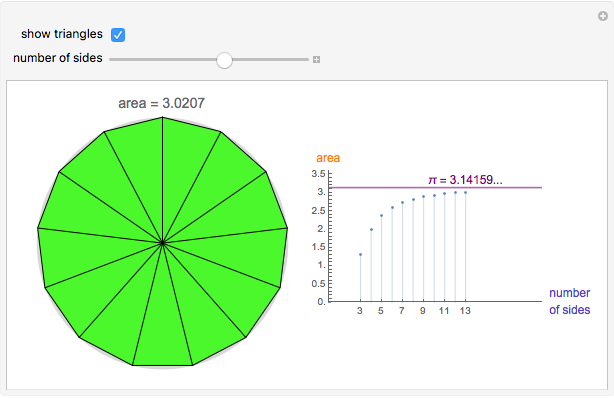
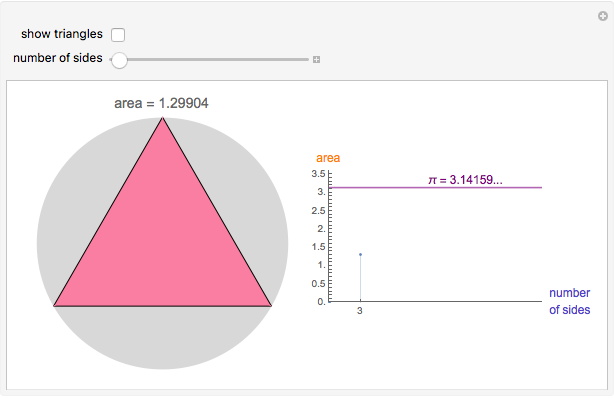
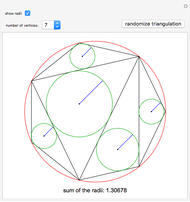
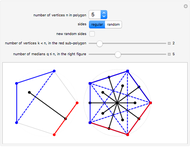
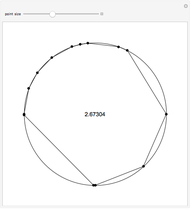
Increase the number of sides of the polygon to see it approximate the unit circle. As the number of sides increases, the area of the polygon approximates the area of a circle with increasing accuracy, showing that the value of π can be estimated with regular polygons.
Contributed by: Rob Morris (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
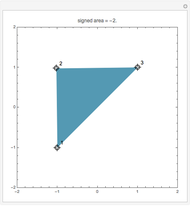
An n-sided regular polygon can be broken up into n equally-sized triangles; the area of the polygon is simply the area of one triangle multiplied by the number of triangles (n). By increasing the number of sides of the regular polygon, it begins to approximate a circle. Thus, a good approximation to the area of a circle can be found by simply finding the area of a single triangle!
Archimedes originally used a similar method over 2200 years ago to calculate the value of π to two decimal places.
Permanent Citation
"Approximating Pi with Inscribed Polygons"
http://demonstrations.wolfram.com/ApproximatingPiWithInscribedPolygons/
Wolfram Demonstrations Project
Published: March 7 2011