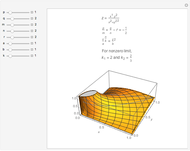
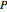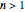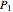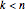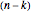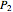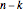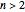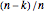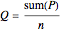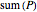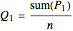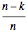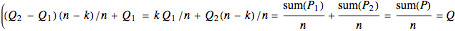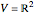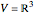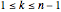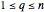The median theorem for polygons is a generalization of the median theorem for triangles.
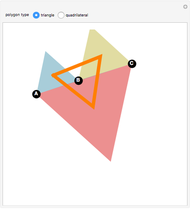
A median of a triangle is a line segment from a vertex to the midpoint of its opposite side.
The median theorem for triangles: The medians of a triangle intersect in a point that is two-thirds of the way from a vertex to the midpoint of its opposite side.
The midpoint and medians of an  -gon may be defined inductively.
-gon may be defined inductively.
The midpoint of a 1-gon (a point) is the point itself.
The midpoint of a 2-gon (a line segment) is the midpoint of the line segment, the point equidistant from its endpoints.
A median of an  -gon
-gon 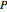 ,
, 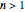 , is a line segment from the midpoint of a
, is a line segment from the midpoint of a  -gon
-gon 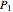 defined by
defined by  of the vertices of
of the vertices of 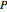 ,
, 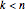 , and the midpoint of a complementary
, and the midpoint of a complementary 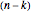 -gon
-gon 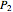 formed from the other
formed from the other 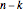 vertices of
vertices of 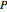 . A 2-gon has just one median, the 2-gon itself.
. A 2-gon has just one median, the 2-gon itself.
The midpoint of an  -gon,
-gon, 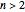 , is the intersection of any two of its medians.
, is the intersection of any two of its medians.
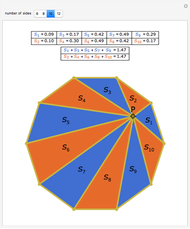
The median theorem for polygons: The midpoint of an  -gon is well defined; its medians all intersect in a point. Its midpoint is
-gon is well defined; its medians all intersect in a point. Its midpoint is 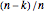 of the way from the midpoint of a
of the way from the midpoint of a  -subgon to the midpoint of a complementary
-subgon to the midpoint of a complementary 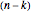 -subgon.
-subgon.
Proof: Let 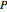 be an
be an  -gon defined by
-gon defined by  points in a vector space
points in a vector space 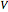 . The midpoint of
. The midpoint of 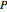 is
is 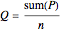 , where
, where 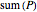 is the vector sum of the vertices of
is the vector sum of the vertices of 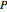 . This point satisfies the definition.
. This point satisfies the definition.
Let 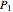 and
and 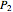 be complementary
be complementary  and
and 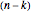 subgons. Let
subgons. Let 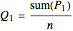 and
and  .
.
The point 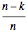 of the way from
of the way from 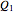 to
to 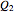 is
is
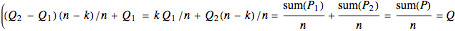 .
.
With 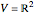 or
or 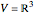 , the median theorem is established for polygons in the plane or in three-space.
, the median theorem is established for polygons in the plane or in three-space.
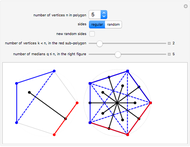
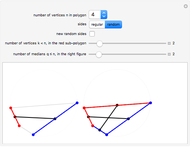
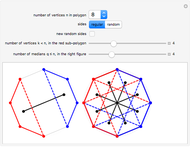
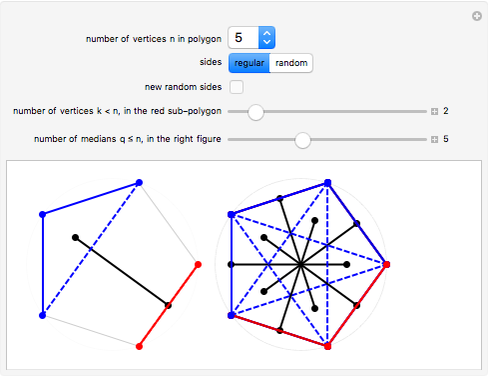
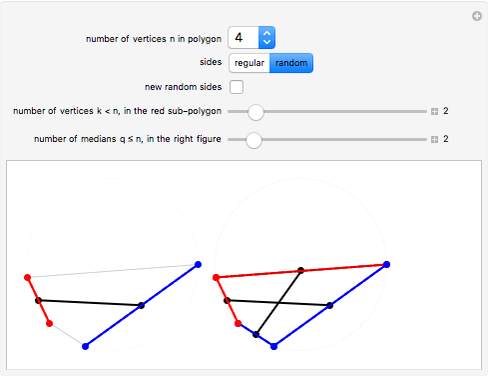
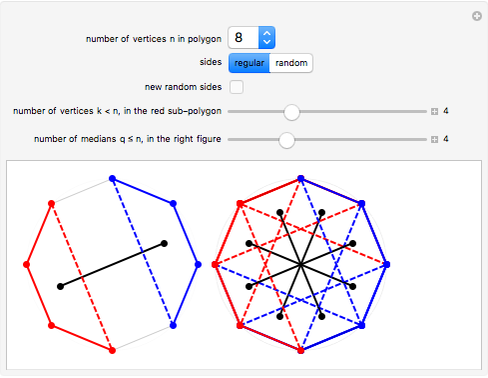
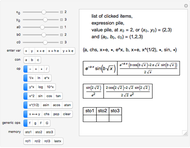
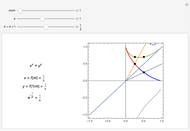
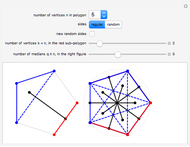
This Demonstration illustrates the median theorem for polygons with vertices on a circle, for both regular polygons and polygons with randomly chosen sides. Complementary subgons are colored red and blue. If you choose random sides, click "new random sides" to obtain a polygon of your liking. When you change  , you need to click at least once to get an
, you need to click at least once to get an  -gon.
-gon.
For a given  , you can choose the number of vertices
, you can choose the number of vertices  for the red subgon,
for the red subgon, 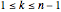 and the number of complementary subgons and medians
and the number of complementary subgons and medians  to be displayed simultaneously in the right figure. The left figure displays the
to be displayed simultaneously in the right figure. The left figure displays the  red/blue subgons with its median,
red/blue subgons with its median, 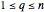 .
.
[less]