Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bisection of Segments by the Sides of a Triangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

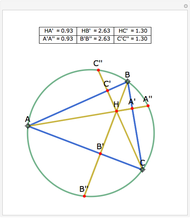
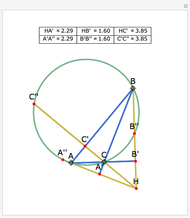
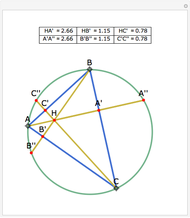
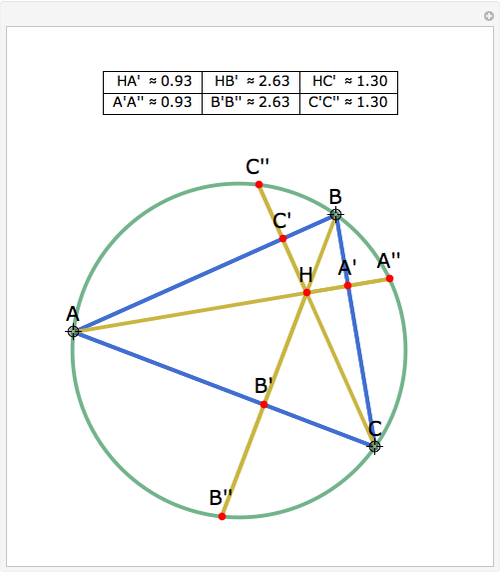
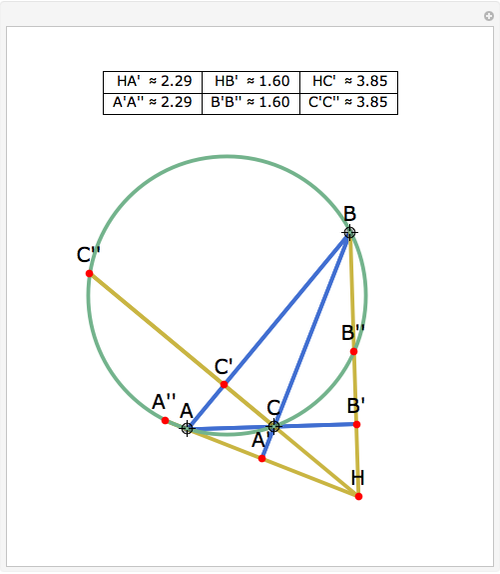
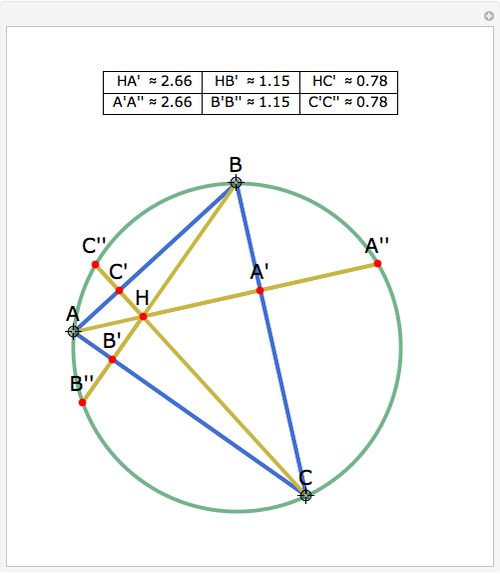
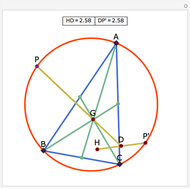
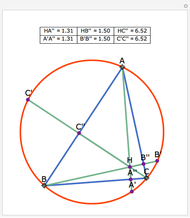
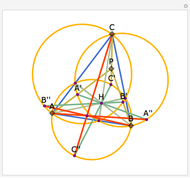
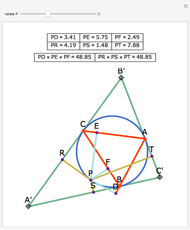
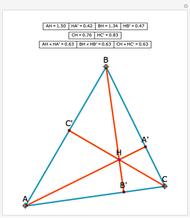
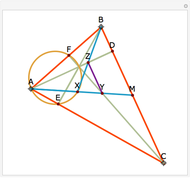
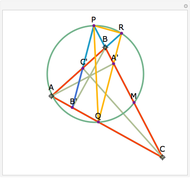
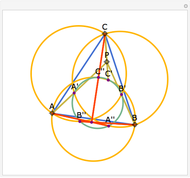
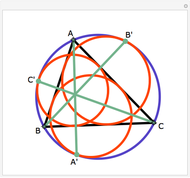
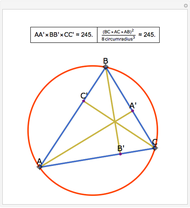
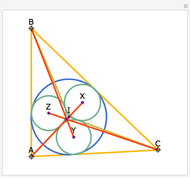
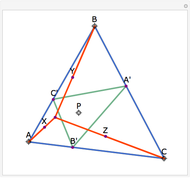
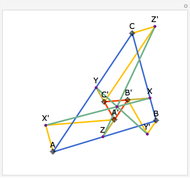
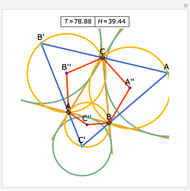
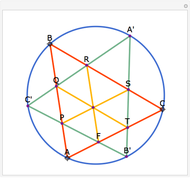
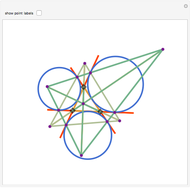
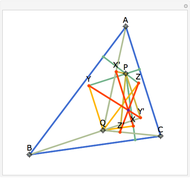
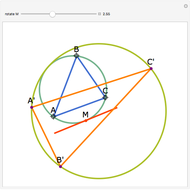
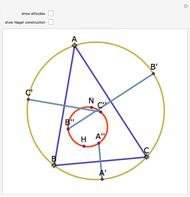
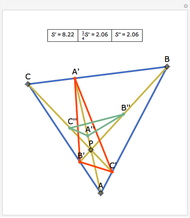
Let ABC be a triangle with orthocenter H, and let the feet of the altitudes be A', B' and C'. Let the extensions of the altitudes intersect the circumcircle a second time at A'', B'', and C''. Then HA' = A' A'', HB' = B' B'', and HC' = C' C''.

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

See Theorem 178 in N. Altshiller-Court, College Geometry, 2nd ed., Mineola, NY: Dover, 2007 p. 95.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send