Chebyshev Collocation Method for 2D Boundary Value Problems

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
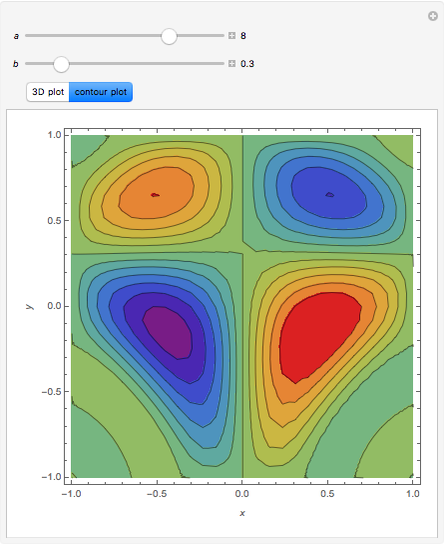
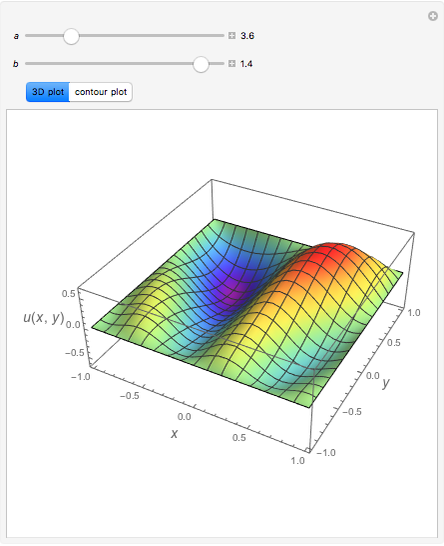
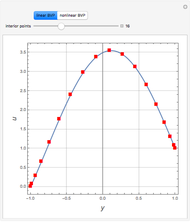
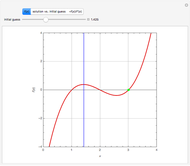
Consider the 2D boundary value problem given by 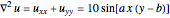 , with boundary conditions
, with boundary conditions 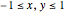 and
and 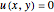 . You can set the values of
. You can set the values of  and
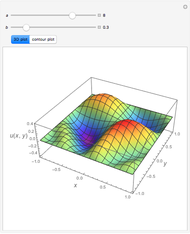
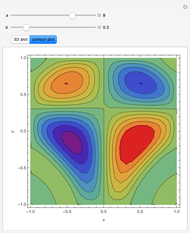
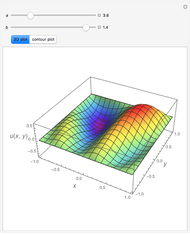
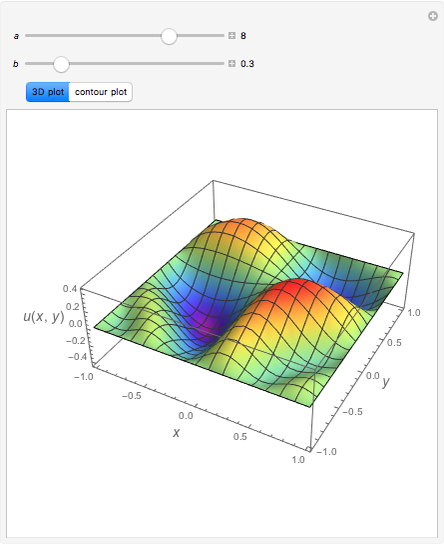
and  . Using this Demonstration, you can solve the PDE using the Chebyshev collocation method adapted for 2D problems. The solution is shown as either a 3D plot or a contour plot.
. Using this Demonstration, you can solve the PDE using the Chebyshev collocation method adapted for 2D problems. The solution is shown as either a 3D plot or a contour plot.
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the discrete Chebyshev–Gauss–Lobatto case, the interior points are given by 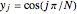 . These points are the extrema of the Chebyshev polynomial of the first kind,
. These points are the extrema of the Chebyshev polynomial of the first kind, 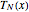 .
.
The 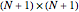 Chebyshev derivative matrix at the quadrature points is an
Chebyshev derivative matrix at the quadrature points is an 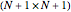 matrix
matrix  given by
given by
 ,
,  ,
,  for
for 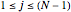
and
 for
for 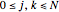 and
and  ,
,
where 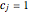 for
for 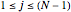 and
and 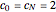 .
.
The discrete Laplacian is given by 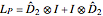 , where
, where  is the
is the  identity matrix,
identity matrix,  is the Kronecker product operator,
is the Kronecker product operator,  , and
, and  is
is  without the first row and first column.
without the first row and first column.
Reference
[1] L. N. Trefethen, Spectral Methods in MATLAB, Philadelphia: SIAM, 2000.
Permanent Citation