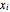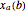Circulant Ring Systems

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
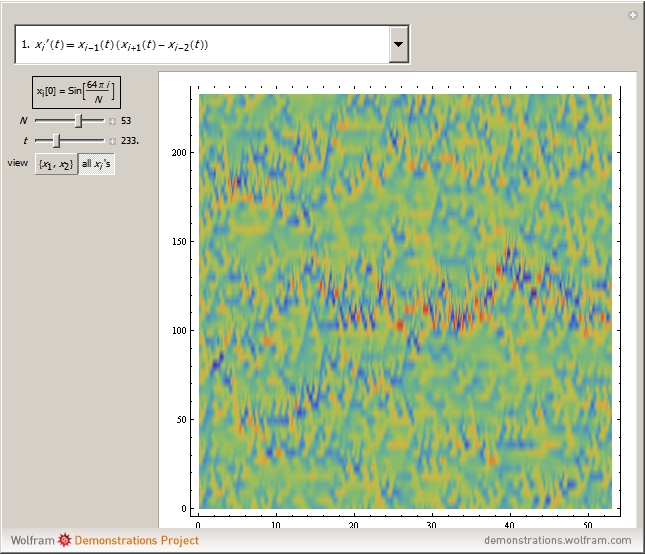
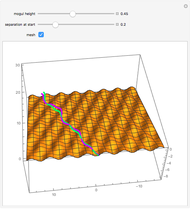
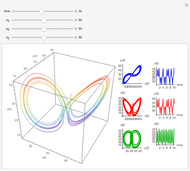
Consider a set of elements linked to form a ring. Examples might be masses joined by springs, nodes in a circular communication system, or circuit components. The equation for the state of the 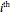 element depends on the state of its nearby neighbors, for instance the ones at positions
element depends on the state of its nearby neighbors, for instance the ones at positions  ,
,  , and
, and 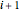 in the first equation. (The position of an element is taken modulo
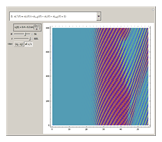
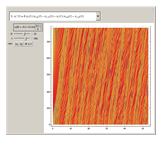
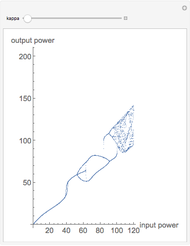
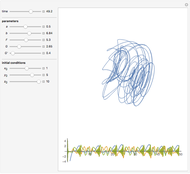
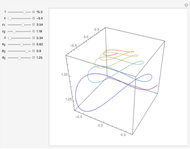
in the first equation. (The position of an element is taken modulo  .) This construction forms a circulant ring system analogous to systems arranged linearly, such as the Lotka–Volterra systems of equations or equations arising from neural networks, cubic oscillators, and so on. Starting from an initial condition for the state of each element, the trajectories of the elements are often chaotic.
.) This construction forms a circulant ring system analogous to systems arranged linearly, such as the Lotka–Volterra systems of equations or equations arising from neural networks, cubic oscillators, and so on. Starting from an initial condition for the state of each element, the trajectories of the elements are often chaotic.
Contributed by: Enrique Zeleny (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] J. C. Sprott, Elegant Chaos: Algebraically Simple Chaotic Flows, Singapore: World Scientific, 2010.
Permanent Citation