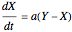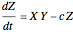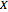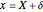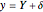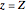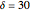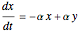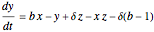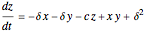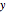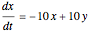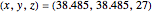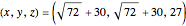Chemical Reactions Described by the Lorenz Equations
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
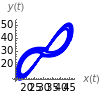
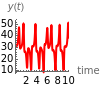
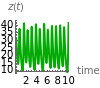
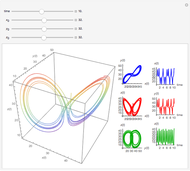
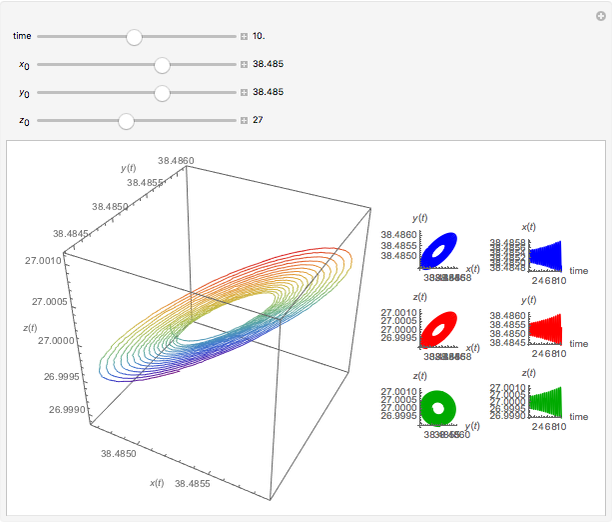
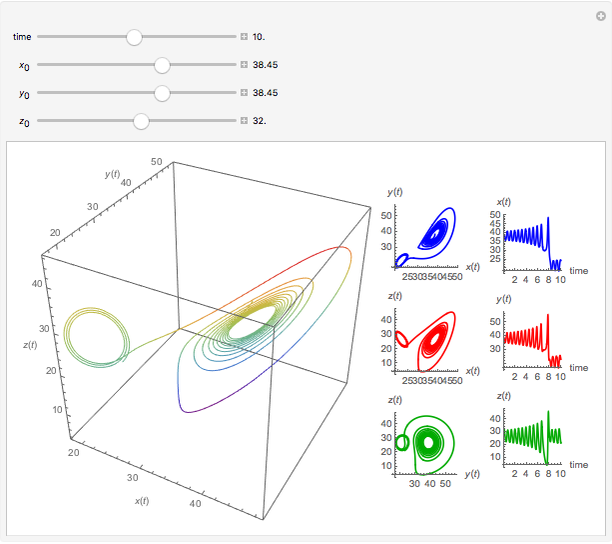
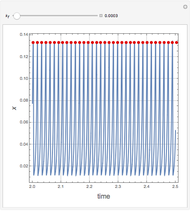
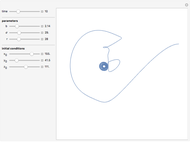
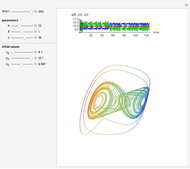
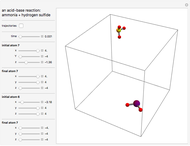
This Demonstration analyzes the behavior of a chemical reaction scheme that is described by the Lorenz equations:
[more]
Contributed by: Clay Gruesbeck (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] D. Poland, "Cooperative Catalysis and Chemical Chaos: A Chemical Model for the Lorenz Equations," Physica D 65(1–2), 1993 pp. 86–99. doi:10.1016/0167-2789(93)90006-M.
Permanent Citation