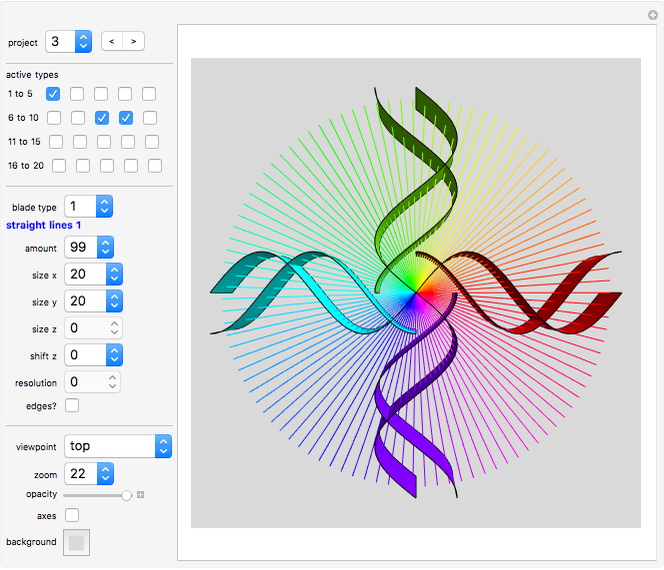
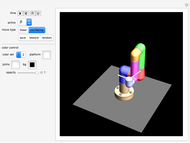
Color Blades

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
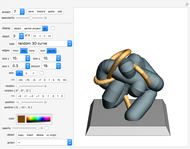
The elegantly curved blades of turbines were the inspiration for this tool.
[more]
Contributed by: Karl Scherer (June 2014)
Open content licensed under CC BY-NC-SA
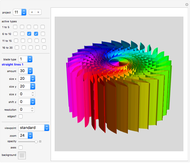
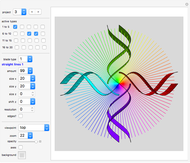
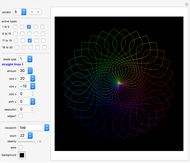
Snapshots
Details
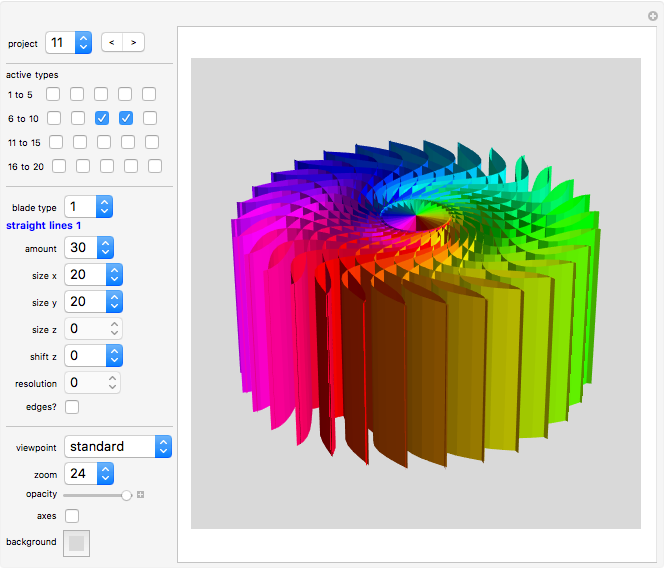
Controls
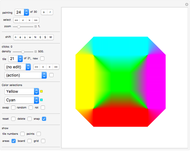
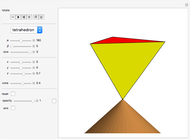
"project" gives you 20 examples of how you can combine various blade types. Study the given projects to learn from them.
Some projects (such as project 16) take a few seconds to load because of their high resolution.
"active types" lets you select which blade designs are displayed at the moment. When you start, select and vary only one blade type at a time. Then combine types by activating more than one blade type.
Combining several blade designs creates many fascinating color effects. Explore!
Blade Types and Their Controls
Blade types 11–20 are identical to blade types 1–10; therefore, only blade types 1–10 are described here.
Blade Types 1 and 2
"straight lines 1", "straight lines 2": lines starting from the origin 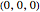 with their ends lying on an ellipse.
"amount": number of lines.
"size x": size of the
with their ends lying on an ellipse.
"amount": number of lines.
"size x": size of the  axis of the ellipse of "spokes".
"size y": size of the
axis of the ellipse of "spokes".
"size y": size of the 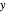 axis of the ellipse of "spokes".
"size z": input disabled.
"shift z": shift the ellipse of "spokes" in the
axis of the ellipse of "spokes".
"size z": input disabled.
"shift z": shift the ellipse of "spokes" in the  direction.
"resolution": input disabled.
"edges?": click to have the endpoints of the lines connected with a colored polygon.
direction.
"resolution": input disabled.
"edges?": click to have the endpoints of the lines connected with a colored polygon.
Blade Type 3
"sine": sine curves in the  -
-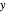 plane starting from the origin
plane starting from the origin 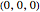 with their ends lying on a circle.
"amount": number of curves.
"size x": radius of the circle.
"size y": height of the sine curve in the x-y plane: if
with their ends lying on a circle.
"amount": number of curves.
"size x": radius of the circle.
"size y": height of the sine curve in the x-y plane: if  is "size y",
is "size y", 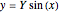 "size z": deformation of sine curve in the
"size z": deformation of sine curve in the  direction.
"shift z": shift the blades in the
direction.
"shift z": shift the blades in the  direction.
"resolution": with low resolution the sine curve will be a polygon rather than a curve.
"edges?": input disabled.
direction.
"resolution": with low resolution the sine curve will be a polygon rather than a curve.
"edges?": input disabled.
Blade Type 4
"cosine": cosine curves in the x-y plane starting from the origin 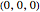 with their ends lying on a circle.
"amount": number of curves.
"size x": radius of the circle.
"size y": height of the sine curve in the x-y plane: if
with their ends lying on a circle.
"amount": number of curves.
"size x": radius of the circle.
"size y": height of the sine curve in the x-y plane: if  is "size y",
is "size y",  "size z": deformation of cosine curve in the
"size z": deformation of cosine curve in the  direction.
"shift z": shift the blades in the
direction.
"shift z": shift the blades in the  direction.
"resolution": with low resolution the cosine curve will be a polygon rather than a curve.
"edges?": input disabled.
direction.
"resolution": with low resolution the cosine curve will be a polygon rather than a curve.
"edges?": input disabled.
Blade Type 5
"wavy disk": disk warped in the z direction.
"amount": twice the number of maxima shown (amount set to 10 produces five maxima)
"size x": radius of the disk.
"size y": input disabled.
"size z": deformation of disk in the  direction.
"shift z": shift the blades in the
direction.
"shift z": shift the blades in the  direction.
"resolution": with low resolution the rim of the disk will be a polygon rather than a circle.
"edges?": click to have the disk's rim painted black.
direction.
"resolution": with low resolution the rim of the disk will be a polygon rather than a circle.
"edges?": click to have the disk's rim painted black.
Blade Types 6 and 7
"straight walls 1", "straight walls 2": walls starting from the z axis with their ends lying on a circle.
"amount": number of walls.
"size x": size of the circle.
"size y": input disabled.
"size z": height of walls (extending in the z direction).
The extraction in the  direction is executed on both sides of the
direction is executed on both sides of the  -
-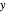 plane, hence the blades are half below and half above the plane. You can change this, however, with the "shift z" control, which shifts the blades of the currently edited blade type along the
plane, hence the blades are half below and half above the plane. You can change this, however, with the "shift z" control, which shifts the blades of the currently edited blade type along the  axis.
"shift z": shift the walls in the
axis.
"shift z": shift the walls in the  direction.
"resolution": input disabled.
"edges?": click to have the rims of the walls colored black.
direction.
"resolution": input disabled.
"edges?": click to have the rims of the walls colored black.
Blade Type 8
"sine walls": sine curves extracted into the z direction.
"amount": number of curves.
"size x": radius of the circle.
"size y": height of the sine curve in the x-y plane: if  is "size y",
is "size y", 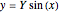 "size z": height of walls (extending in the
"size z": height of walls (extending in the  direction).
"shift z": shift the blades in the
direction).
"shift z": shift the blades in the  direction.
"resolution": with low resolution the sine curve will be a polygon rather than a curve.
"edges?": click to have the rims of the walls colored black.
direction.
"resolution": with low resolution the sine curve will be a polygon rather than a curve.
"edges?": click to have the rims of the walls colored black.
Blade Type 9
"cosine walls": cosine curves extracted in the  direction.
"amount": number of curves.
"size x": radius of the circle.
"size y": height of the sine curve in the x-y plane: if
direction.
"amount": number of curves.
"size x": radius of the circle.
"size y": height of the sine curve in the x-y plane: if  is "size y",
is "size y", 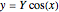 "size z": height of walls (extending in the
"size z": height of walls (extending in the  direction).
"shift z": shift the blades in the
direction).
"shift z": shift the blades in the  direction.
"resolution": with low resolution the sine curve will be a polygon rather than a curve.
"edges?": click to have the rims of the walls colored black.
direction.
"resolution": with low resolution the sine curve will be a polygon rather than a curve.
"edges?": click to have the rims of the walls colored black.
Blade Type 10
"triangles": triangles in the  -
-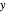 plane arranged around the origin
plane arranged around the origin 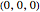 with two points lying on an ellipse.
"amount": number of wave maxima in the
with two points lying on an ellipse.
"amount": number of wave maxima in the  direction.
"size x":
direction.
"size x":  axis of the ellipse.
"size y":
axis of the ellipse.
"size y": 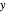 axis of the ellipse.
"size z": "waviness" in the
axis of the ellipse.
"size z": "waviness" in the  direction.
"shift z": shift the blades in the
direction.
"shift z": shift the blades in the  direction.
"resolution": double the number of triangles (a resolution of 40 produces 20 triangles).
"edges?": click to have the rims of the triangles colored black.
direction.
"resolution": double the number of triangles (a resolution of 40 produces 20 triangles).
"edges?": click to have the rims of the triangles colored black.
Global Controls
"viewpoint" lets you look at your design from various directions. It describes the position of the observer.
"zoom" lets you zoom in or out. More specifically, the viewpoint (a vector in three dimensions) is multiplied by the "zoom" value and shortened by a factor of 20. Hence small zoom values mean a closer view. If zoom is set to 1, we are 20 times closer to the origin than when zoom is set to 20. Zooming in often adds to the attractiveness of a design.
"opacity" applies to all parts of the project.
"axes" displays the  axis in green, the
axis in green, the 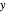 axis in red, and the
axis in red, and the  axis in blue. The arrow tips are 20 units away from the origin.
axis in blue. The arrow tips are 20 units away from the origin.
Permanent Citation