Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tracking and Separation (Visual Depth Perception 11)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

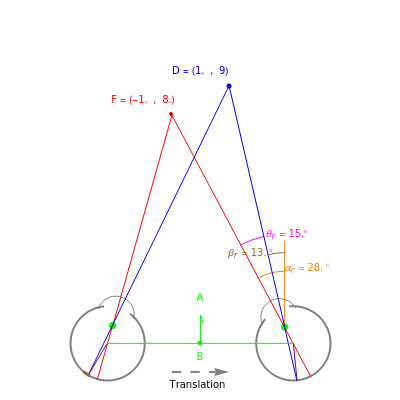
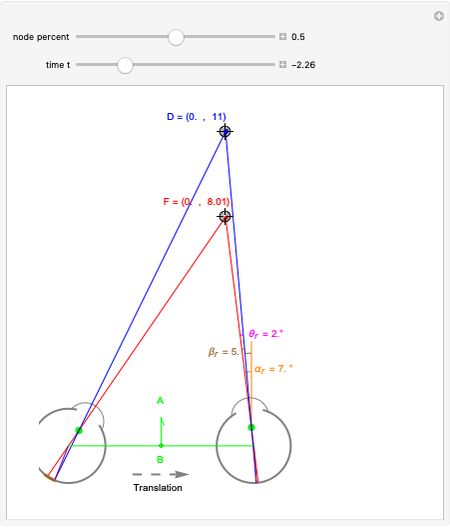
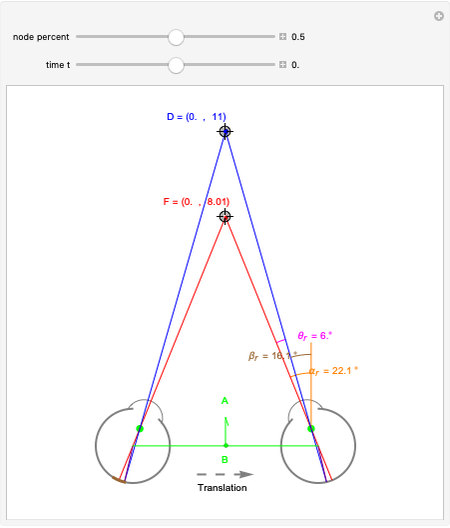
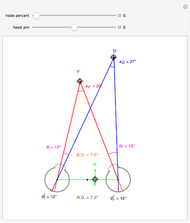
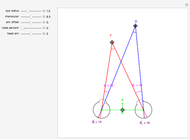
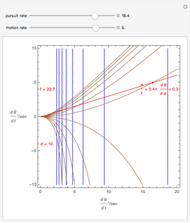
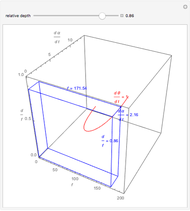
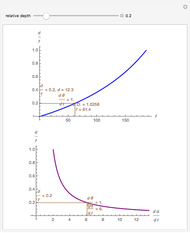
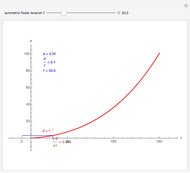
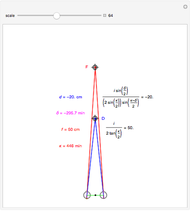
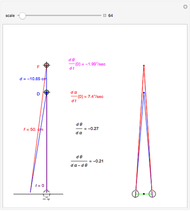
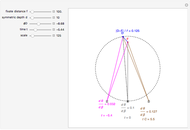
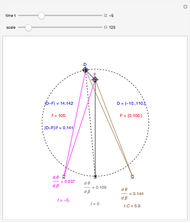
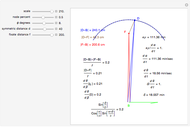
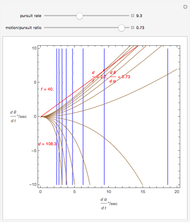
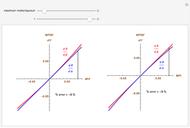
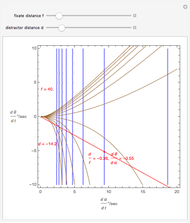
We study the case of an observer moving at right angles to the aim of the head, fixing his eyes on a (fixate) point F and also observing a distractor D. The important angles for depth perception by motion parallax are and . The angle is mathematically helpful.

[more]

To animate motion in time, click the [+] next to the "time " slider and click play [>]. The changing position of the distractor on the retina is "motion parallax".

[less]

Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

$Failed
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send